小学算数の面積の求め方と公式一覧！四角形・長方形の性質や円の計算方法まで解説！

最初に小学校で習う図形の面積の特徴と重要性をご説明します。

図形の面積には種類が多いの？

小学校で学ぶ図形の面積の種類や公式は多くはありません。基本は三角形・四角形と円です。そして基本の形を少し変えた形ですが、覚えるのはそれほど難しくありません。

ただ、小学校で学ぶ図形は先々の勉強の土台となる基本中の基本です。確実にマスターすべきものです。

お子さんが面積の形や計算に苦手意識を持たないように、まずは図形に慣れさせることから始めましょう。

面積の理解は体積にもつながる

図形の面積の計算は、長さをベースにしており、さらに体積の計算へとつながるものです。

つまり、面積をきちんと理解できれば応用が広がっていく大事なステップになります。

逆に面積でつまずくと先々苦労することになりかねません。最初は戸惑いを感じるかもしれませんが、興味を持たせて頑張るように仕向けることが大切です。

それでは早速、四角形や長方形の基本的な面積の求め方・公式からみていきましょう。

三角形の面積

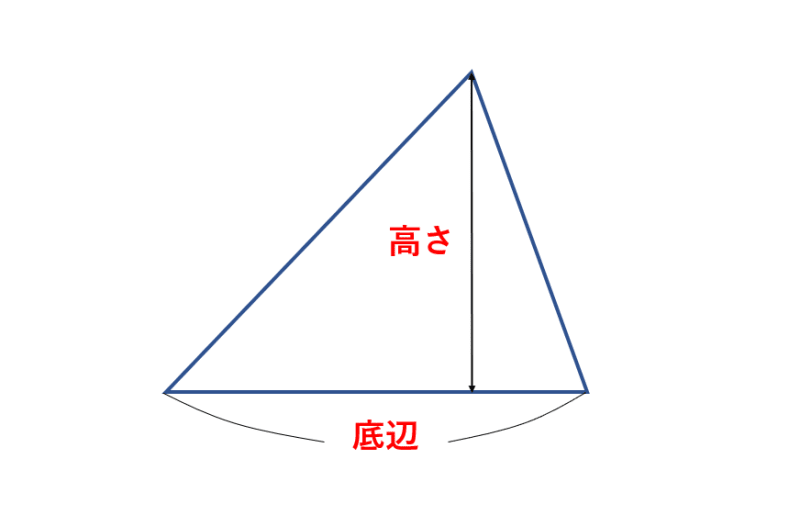
三画形の面積は、

底辺×高さ÷2

で求めることができます。

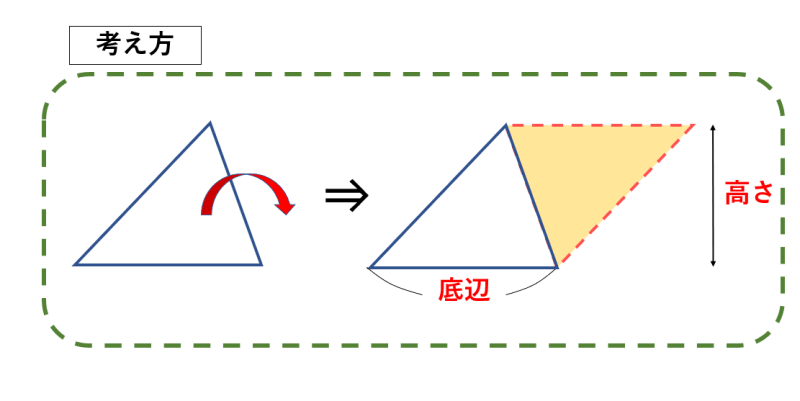
三角形は平行四辺形を対角線で切って半分にした形です。同じ形の三角形を逆さまにして2つを合わせてみるとすぐ分かります。

ですから、まず平行四辺形の面積（底辺×高さ）を計算して、その半分にするのです。三角形であればどんな形でも、この公式で計算できます。

円の面積

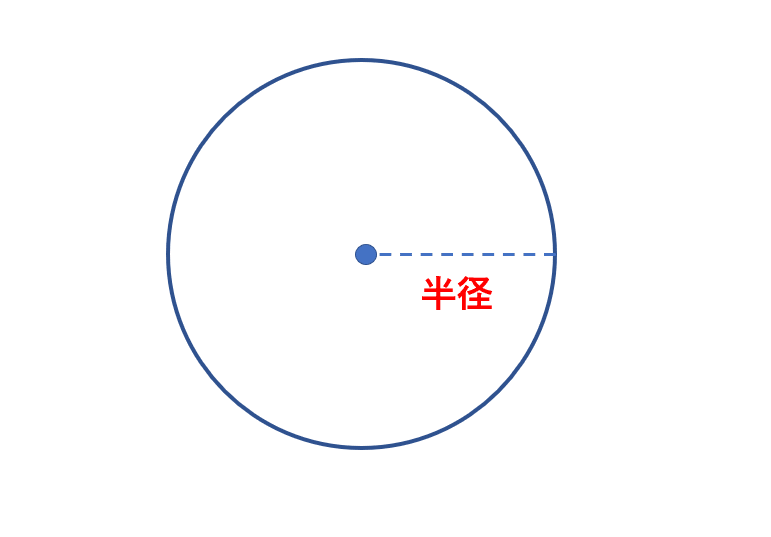
円の面積は、

半径×半径×3.14

で求めることができます。なお、3.14のことを円周率といい、πと表すことも多いです。

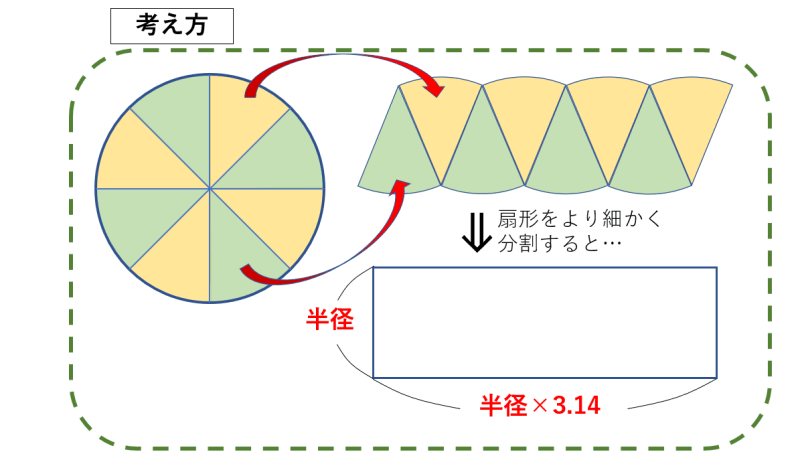
円を細かくおうぎ形に切って、交互に逆さまに並べていくと長方形になります。

辺の長さは、短い方が円の半径、長い方は円周の半分（半径×3.14）になります。短い辺（半径）と長い辺（半径×3.14）の長さを掛けて円の面積になるのです。

なぜ3.14倍（あるいはπ倍）にするのかは覚えるしかありませんが、暗記しておくと役立ちます。

正方形・長方形の面積

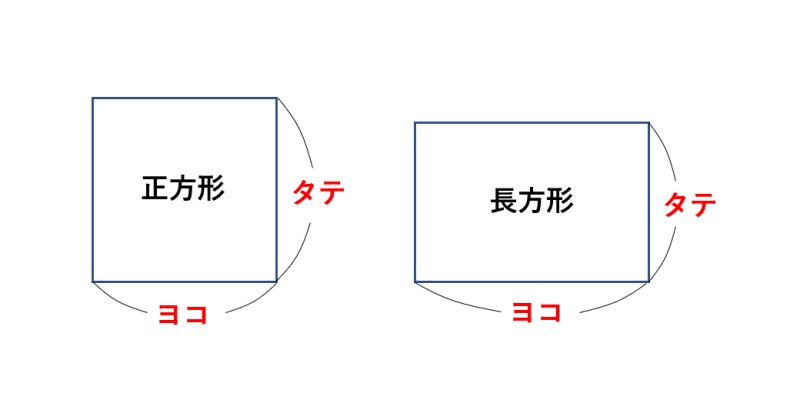
正方形・長方形は2組の平行な対辺が垂直に交わり、4つの角がすべて直角になっている四角形です。

ですから、正方形・長方形の面積は、

縦の長さ×横の長さ

で求めることができます。

正方形は4つの辺が同じ長さなので、

一辺の長さ×一辺の長さ

と置き換えることもできますが、正方形の公式だけを別に覚える必要性はありません。

平行四辺形の面積

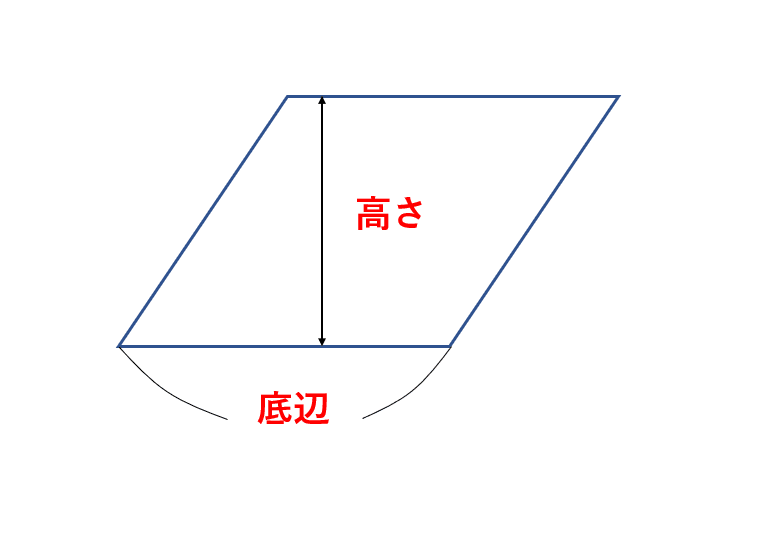
平行四辺形は2組の平行な対辺が交わりますが、4つの角は直角とは限りません。

平行四辺形の面積は、

底辺×高さ

で求められます。

平行四辺形を底辺上の1点から引いた垂線で切り、切った部分を反対側に移動すると長方形になるからです。

底辺は、4つの辺のどれを選んでもよいです。高さは、選んだ底辺上の1点から引いた垂線の長さになります。垂線は、1つの線（辺）から直角にまっすぐに引いた線です。

ひし形の面積

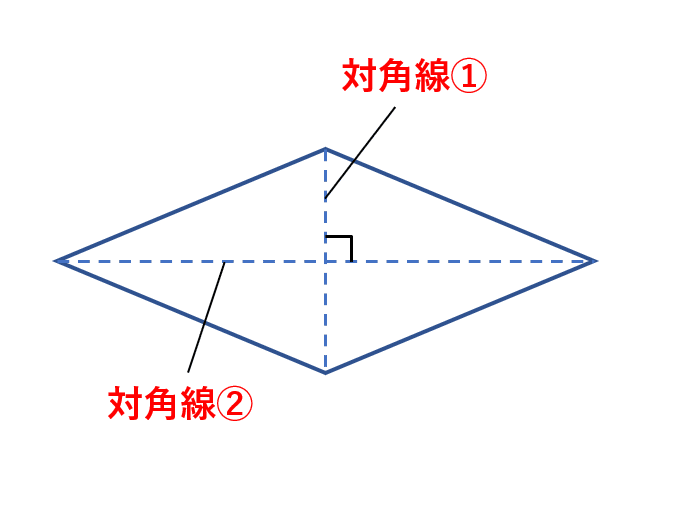ひし形は、4つの辺がすべて同じ長さである四角形です。 ひし形の対角線は直交しています。

ひし形の面積は、

対角線×もう一方の対角線÷2

で求められます。

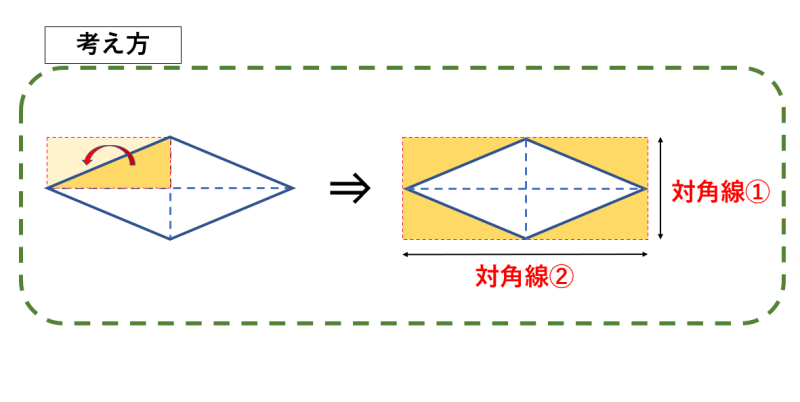
ひし形は横の対角線を横の辺、縦の対角線の半分を縦の辺とした長方形に変えられるからです。ひし形を対角線で4つに切ってみると分かります。

ひし形は平行四辺形の1つです。辺の長さと高さが分かっていれば、

底辺×高さ

で面積を求めることもできます。

台形の面積

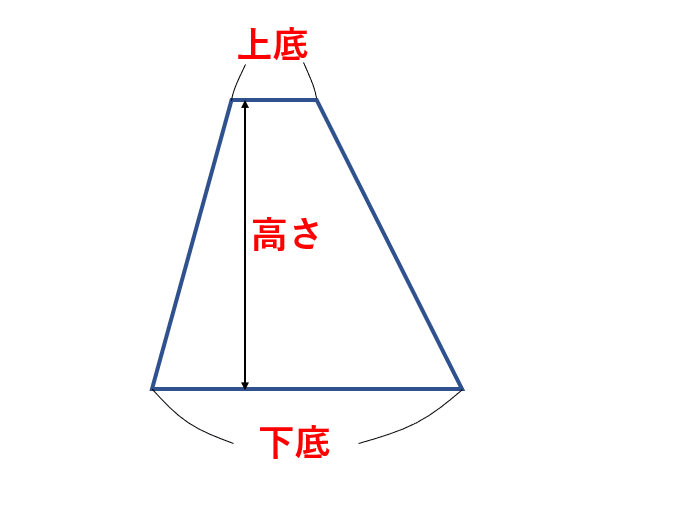台形は、向かい合う辺の少なくとも1組が平行な四角形です。向かい合う辺を底辺、一方を上底、他方を下底といいます。

台形の面積は、

(上底+下底)×高さ÷2

で求められます。

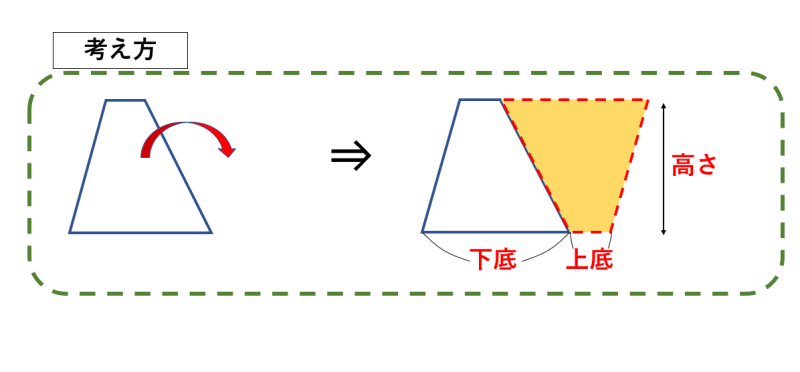
台形に同じ台形を逆さまにして組み合わせると平行四辺形ができます。ですから 台形の面積はできた平行四辺形の半分ということになります。

この平行四辺形の面積は「底辺（上底+下底）×高さ」ですので、上の公式になります。

問題

1. 直径10cmの円の面積（ただし、円周率をπとする）
2. 上底2cm、下底4cm、高さ10cmの台形の面積
3. 一方の対角線の長さが8cm、一辺の長さが5cmのひし形の面積（発展・中学生向け）
4. 底辺の長さが6cm、残りの2辺の長さが5cmの二等辺三角形の面積（発展・中学生向け）

解答

1. 25π㎠
2. 30㎠
3. 24㎠
4. 12㎠

1番と2番は、単に公式に当てはめるだけで解ける問題です。小学生のうちはまずは公式をサクサク使いこなせるようになりましょう。

3番と4番は先取り学習をしている小学生向けの問題です。三平方の定理を上手に用いることで解くことができます。

3番の解説

公式を用いるために、もう一方の対角線の長さを求めます。

ひし形に対角線を引いてできる、小さな4つの直角三角形のうちの1つに注目すると、斜辺が5cmで、もう一辺の長さが4cmであることが分かります。

残る1辺の長さをxとして、この直角三角形で三平方の定理を用いると、

x^2 = 5^2 - 4^2

これを解いて、x=3となります。つまり、もう一方の対角線の長さは3×2の6cmであることが分かります。

したがって求めるひし形の面積は

8×6÷2=24（㎠）となります。

4番の解説

二等辺三角形の頂点から垂直二等分線を下ろすと、斜辺の長さが5cm、もう一辺の長さが3cmの直角三角形が2つできます。

したがって、二等辺三角形の高さをhとすると、三平方の定理より

h^2 = 5^2 - 3^2

これを解いて、h＝4となります。

よって求める二等辺三角形の面積は

6×4÷2=12（㎠）となります。

この章では面積を出すときのコツをご紹介します。

わかりにくい時は方眼紙で学習

面積は感覚的に分からないというお子さんもいます。そういう時は方眼紙に図を書いてみるとよいです。

方眼紙の目のサイズはいくつかありますが、1マスが１平方センチメートルの方眼紙を使えば、実際の面積の大きさを自分の目で確認して実感できます。

図形を見ながら形を移動させたり、切って移すこともできるので、 面積の公式が視覚的によく分かり最適です。

公式は暗記する

小学校で習う公式は先々の勉強の土台になるので、誰もが必ず覚えるべきものです。

公式を覚えていないとテストの時に迷うなど大きなハンディになります。長く続くテストを戦い抜くためにも、公式の暗記は必須です。

ただ、公式は暗記すればそれでよいというものではありません。なぜそうなるのか、意味をきちんと理解することが大切です。

公式の意味を理解して暗記しておけば中学以降の算数・数学も分かりやすくなり、応用の可能性が広がります。

面積問題は中学受験でも頻出

面積問題は、中学受験でよく出題されます。問題のパターンはいろいろあります。

例えば、円をおうぎ形にする、四角形を組み合わせる、図形の一部を移動して加えたり・除外したりするなどの問題があります。

一見難しそうですが、切り口さえ見つければ意外と簡単に解ける問題も多いです。

図形はパズルのようなものです。大事なことは問題と解き方のパターンに慣れることです。ゲーム感覚で興味をもって楽しみましょう。

この章では、小学算数の中学・高校数学への応用についてご説明します。

三平方の定理

まず、ピタゴラスの定理ともいわれる三平方の定理についてご説明します。

これは直角三角形の定理です。直角をはさむ2辺の長さをa・b、斜辺の長さをcとすると、次の公式が成り立ちます。

三平方の定理　a^2+b^2=c^2

平方とは「2乗する」ということを指し、3辺の長さをそれぞれ2乗するので「三平方の定理」と言います。.

2辺の長さが分かれば残りの一辺の長さを求めることができるので、覚えておくと大変便利な公式です。

ヘロンの公式・三角関数

三角形の面積の求め方には、他にヘロンの公式と三角関数の利用もあります。

ヘロンの公式

ヘロンの公式は、三角形の3辺の長さから面積を求める公式です。

3辺の長さが a・b・cの三角形の面積Sは、次の式で表されます。

s＝(a+b+c)/2とすると、

三角形の面積 S=√s(s−a)(s−b)(s−c)

3辺の長さが分かれば簡単に面積を求めることができるので、覚えておくと便利です。

三角関数

三角関数を使って三角形の面積を求める公式もあります。

三角形の面積 S=1/2・a ・b sinθ

aは底辺の長さ、b sinθは三角形の高さです。

こちらは、学校で習わないうちは「こんな方法もあるんだな」という程度に覚えておくだけでよいです。

楕円の面積

楕円の面積の計算の仕方も見ておきましょう。楕円は簡単にいうと、円を一定の方向につぶした形あるいは逆に伸ばした形です。

楕円の面積の公式は、次ようになります。

楕円の面積 S=π・a・b

楕円は半径aの円を縦軸方向に b/a倍縮小（拡大）した図形と考えることができます。

ですから、円の面積公式（π・r・r）の応用と考えると覚えやすいです。

この章では、面積の問題が苦手な小学生におすすめの教材をご紹介します。

まずは学校の教材を活用する

小学校の勉強は基礎的なことを身に付けることが目的です。

受験を目的に塾に通うことや勉強を進めることはよいことですが、学校の教材を活用するだけで十分です。特別の教材はなくても問題ありません。

小学生の時にしかできない遊びの時間も大切にしましょう。いろいろな経験をしておくことは、その後の成長にとって大事なことです。

もちろん学校の勉強や宿題をサボってはいけません。まずは学校の教材・宿題をしっかりこなして基礎を身に付けることを優先しましょう。

中学受験の学習なら受験塾のテキストで学習

中学受験を目指すなら、おすすめの教材は受験塾が独自に作っているテキストです。

大手の受験塾は試験の過去問をしっかり分析して、問題を上手に解ける分かりやすい教材を作っています。

特に難関私立中高一貫校向けのオリジナルテキストは、高いレベルの実力を養うのに最適です。

このようなテキストで学習してしっかり自分のものにすることが、合格への近道になります。

通信教育もおすすめ

最近の通信教育ではタブレット学習ができるものが増えています。 お子さんが楽しんで学習しやすくなるため、1人での学習でも知らず知らずのうちに実力が向上します。

算数が苦手なお子さんも苦手を克服して勉強するモチベーションがわき、実力を伸ばす意欲の高いお子さんにも最適です。

おすすめの通信教育について、詳しくはこちらの記事で紹介しています。

小学算数で覚えておかなければならい面積の単位についてまとめておきます。

まず長さの単位を確実に覚える

面積の出し方の基本は長さ×長さです。まず長さの単位を確実に覚えましょう。

基本はメートル（m）です。

メートルにキロ（k：1000）、センチ（c：1/100）、ミリ（m：1/1000）を掛けた次の3つも大事です。

• 1km（キロメートル）=1000m

• 1cm（センチメートル）＝1/100m

• 1mm（ミリメートル）＝1/1000m

面積の単位は2つの種類を覚える

面積の単位は長さの単位の2乗（平方）です。基本は次のようになります。

• 1㎢（平方センチメートル）

• 1㎠（平方センチメートル）

• 1㎟（平方ミリメートル）

面積の単位には、もう1つ土地の面積を表すときに使われるアール（a）もあります。

1aは10ｍ四方の正方形の土地の面積です。そして、1aの100倍が1ha（ヘクタール）です。

• 1a（アール）＝100㎡

• 1ha（ヘクタール）＝10000㎡

今回は、小学算数の四角形や長方形などの面積の求め方と公式をまとめてご説明しました。

小学校の間はまだ比較的簡単な内容ですので、難しく考える必要はありません。

ただ、中学・高校と次第に難しくなる数学につながる大事な一歩です。

計算や図形問題、数学が嫌にならないように楽しく勉強することが大切です。

この記事を参考にして基本的な公式をしっかり覚え、自信をもって前向きに取り組むようにしましょう。