小学生の算数の図形問題の克服法は?中学受験で頻出の角度・面積の対策やドリルを紹介
「小学生が苦手な算数の図形問題を克服するにはどうすれば良い?」
「中学受験で頻出の角度や面積の問題の対策法は?」
などと疑問をお持ちの方もいるでしょう。
算数の図形問題が苦手な小学生は非常に多いです。しかし、図形問題は大学入試までずっと付き纏うので小学生のうちに克服しておくのが良いでしょう。
また中学入試では角度や面積の問題が頻出なので、中学受験を目指すなら早急に対策を行う必要があります。
今回は小学生の算数・図形問題の克服法について、中学受験で頻出の角度や面積の問題の対策法やおすすめのドリルなどを解説します。
これを読んで、図形問題が苦手なお子さんの勉強にお役立てください。
小学生の算数・図形問題の克服法をざっくり説明すると
- 身近な図形に触れることから始める
- 実際に作図してみると理解が深まる
- 面積の問題には原理的な理解も必要
このページにはプロモーションが含まれています
小学生の算数の図形問題はつまずきやすい?

算数の図形問題は多くの小学生が苦労する単元です。どうしたら難しい問題でも解けるようになるのか、お悩みの親御さんも多いでしょう。そうした方は以下の内容を参考にしてください。
図形問題が苦手な子供は多い?
図形問題を苦手にしている小学生は大勢います。計算問題などのように機械的に処理できるわけではないので、初見の問題だと考え方が分からず手が付けられないという場合も多いです。
しかし、小学生のうちはそれほど難しい問題が出題されるわけではないので、きちんと練習して解き方に慣れれば、誰でも苦手を克服することができるでしょう。
特に算数が得意ではない子供の場合は、本格的な図形問題を扱うようになる小学3・4年生になったら、後述の内容を参考に練習を行うのがおすすめです。
図形問題は大学入試でも出題されるので、小学生のうちに慣れておくのが良いでしょう。
角度や面積の問題など多様
一口に図形問題と言ってもその内容は様々です。平面図形を面積の問題もあれば、角度を求める問題もあります。
また高学年になれば、立体図形の体積を求める問題も解ける必要が出てきます。
そのため、まずはそれぞれが苦手としている図形問題の内容を把握し、それに合った対処法を考えるのが良いでしょう。例えば、平面図形は問題なく理解できるが、立体図形になると解けなくなるという場合もあります。
それなら立体図形に特化した対策を講じるべきです。一方で図形問題全般が苦手だという場合は、後述するように図形に慣れることから始めると良いでしょう。
中学受験でも頻出
図形問題には教科書の例題で扱うような基礎レベルから難関私立中学入試で出題されるような難関レベルまで、様々な難易度のものが存在します。
基本的には教科書レベルの内容が理解できていれば十分ですが、中学受験を目指すなら難問も解けるようにならないといけません。
特に角度や面積を求める問題、比を使って解く問題は中学入試でも頻出なので、きちんと押さえておきましょう。
中学受験を目指す場合でも、図形問題が苦手ならまずは基礎レベルから始めるのがおすすめです。応用問題は基礎問題の解法を組み合わせれば解けるので、まずは基本的な問題をたくさんこなしましょう。
難しい問題も解けた方がいい?
中学受験をしないなら、難しい図形問題を解けるようになる必要はありません。小学校のテストで難問が出題されることは稀ですし、教科書内容を十分に理解できていれば中学になっても困ることはないでしょう。
しかし、難しい問題を解く練習をすることにもそれなりのメリットがあります。思考力や計算スピード、諦めない粘り強さなどが身に付くでしょう。
ただし、難しい問題ばかりに挑戦して挫折してしまうと、勉強への自信をなくしてしまう恐れもあるので注意が必要です。難問に挑戦させるのは、子供の学力が十分ついてきてからにしましょう。
図形問題の克服方法は?

図形問題の克服には以下の内容を参考にしてください。
身の回りの図形に触れることから
図形問題への苦手意識をなくすには、図形に慣れることが大切です。そのため、まずは身近なものの図形を考えることから始めると良いでしょう。
例えば、ティッシュの箱は全ての面が長方形なので直方体です。平面図形や立体図形を具体的にイメージするにはとても良い教材と言えます。
身の回りのものには他にもたくさん図形が含まれているので、子供と一緒に探してみましょう。最初は三角形や長方形など、簡単なものから始めて、ある程度慣れてきたら鋭角三角形や鈍角三角形などにも注目するべきです。
具体例をたくさん見ることによって、図形問題にもイメージを持ちながら取り組むことができるでしょう。
自分の手を使って学習
図形を自分で書いてみるのもおすすめです。特に立体図形の場合は、作図することによって構造への理解が深まり、頭の中で図形の回転や移動をイメージしやすくなります。
また作図することによって展開図の意味が理解できるようになる子供もいます。
図形問題を解く際にも、理解の一助として作図を行うことは重要なので、すぐに書けるように練習しておいた方が良いでしょう。
基礎情報は覚えるまで練習
図形にある程度慣れてきたら、実際に簡単な問題を解いてみましょう。
図形問題を解くには三角形の内角の和は180度、四角形は360度などの基本事項を覚える必要がありますが、これらは何度も繰り返し練習する中で自然と身に付くでしょう。
問題に図がついている場合は、そこに長さなどの条件を書き込むと理解しやすくなります。
図形問題への抵抗がなくなったら?

図形問題への抵抗感がなくなってきたら、以下の内容を参考にさらなる学習を行いましょう。
面積の問題は原理を理解する
面積の問題には公式を用いますが、どうしてその計算で面積が求められるのかについてもきちんと理解させておくべきです。
原理的な理解を深めることによって、公式が忘れにくくなります。たとえ忘れてしまったとしても、原理を知っていればすぐに思い出せるでしょう。
原理まで理解した状態で演習をこなせば、知識が頭に定着しやすくなります。
単位の換算も重要なポイント
面積の計算には「(辺の長さ)×(辺の長さ)」という工程が含まれるため、左辺と右辺では単位が変化します(㎝→㎠など)。
そのため、左辺と右辺の関係、つまり辺の長さと面積の関係をきちんと理解することが重要です。分かりやすく教えるには、方眼紙を使って面積の変化を可視化してあげると良いでしょう。
また小学4年生では「ha(ヘクタール)」や「a(アール)」など、面積特有の単位を学びます。これに関しては実際の土地の大きさなどを例にとって教えてあげると良いでしょう。
問題の条件は図にする
初歩的な問題では、図が載っていてそれに長さなどの条件が丁寧に書き込まれている場合が多いです。
しかし、問題のレベルが上がってくると、長さなどが書かれていなかったり、そもそも図がないこともあります。
そのため、問題文の内容を自分で図にまとめる習慣を付けさせると良いでしょう。長さや角度などの情報を付け加えたり、図がない場合は自分で作図すれば、問題への理解が深まります。
慣れてきたら問題数をこなす
基本レベルや標準レベルの問題を数多く解けば、解法のパターンを把握することができます。
応用問題もこのパターンを組み合わせることで解くことができるので、まずは問題数をこなして基本的な解き方をマスターすることが重要です。
ただし、応用問題まで解けるようになる必要がありません。小学校のうちは基本的な内容を押さえていれば十分なので、教科書やドリルの問題さえ解ければ良いでしょう。
ボコボコした図形の面積計算は頻出
四角形に穴が空いていたり、四角形を組み合わせたような図形の面積を求めさせる問題は定番です。
それらの面積を求めるには、図形をバラバラにして面積を足し合わせる方法と、大きな図形の面積から小さな図形の面積を引くという方法が考えられます。
「他の解き方も考えてみよう」などと声かけをして、どちらの方法も身に付けさせるのがおすすめです。
一つの問題に対して複数のアプローチをする
ある問題を解くために多角的なアプローチを考えることは有意義です。
子供もある程度問題数をこなしたり、レベルの高い問題に取り組むようになれば、解き方が複数あることに気付くでしょう。その段階になれば、複数の解き方を身に付けさせるべきです。
解法をいくつか持っていれば、新しい問題に取り組む際に解きやすい方法を選択することができます。また難問は基本的な解法を組み合わせて解く必要があるので、引き出しをたくさん持っておいた方が有利です。
小学生向け図形問題3選!

初級
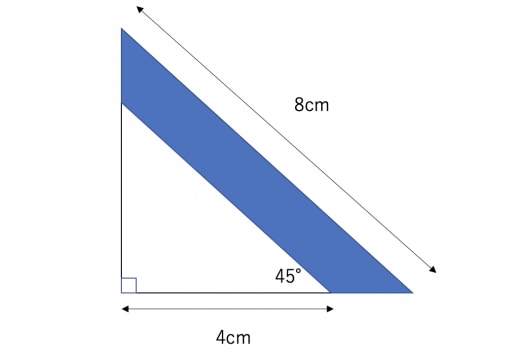
上の図の青色部分の面積は何㎠でしょうか。なお、青色部分を含めた最も大きな三角形は直角二等辺三角形です。
答え
最も大きな三角形の直角の頂点から垂線を下ろせば良い。このとき、この垂線は垂直二等分線になる。
すると、垂線の長さは8÷2=4(cm)と分かるので、
全体の面積は
8×4÷2=16(㎠)
よって求める面積は
16-(4×4÷2)=8(㎠)
中級
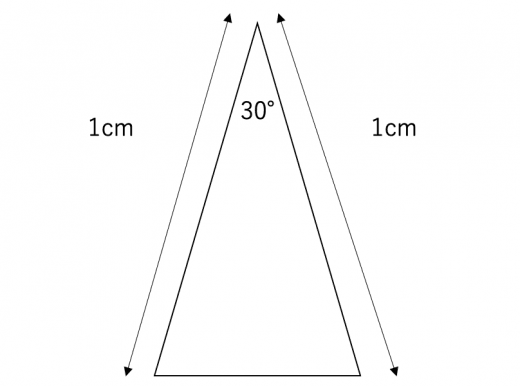
上の三角形の面積を求めよ。
答え

図のように30度ではない(75度の角)を持つ頂点から垂線を下ろすと、求める三角形の底辺1cmとしたときの高さが出る。
この高さを求めれば良い。
垂線と辺がなす角は60度なので、図のようにこれを折り返すことで正三角形が出来上がる。(全ての角が60度)
求める高さは正三角形の1辺の長さの半分なので、0.5cm。
よって求める面積は
1×0.5÷2=0.25(㎠)
上級

四角形ABCDは1辺が5cmの正方形、1マスは1cm×1cmの正方形となっています。
この中に面積が13㎠の正方形を作成してください。
答え
正方形ABCDの面積は25㎠。正方形ABCDの4隅から、合計12㎠を切り取れば良い。
したがって、例えば以下のような正方形が作成できる。

図形問題の対策におすすめ教材はある?

ここからは図形問題の対策におすすめの教材をいくつか紹介します。
学校の教科書やドリルで対策
基本的に小学生のうちは塾に通ったり、市販の参考書や問題集を購入する必要はありません。まずは学校の教材の内容をきちんと理解することが大切だからです。
そのため、自宅では学校の教科書やドリルの問題を使って勉強するのが良いでしょう。先述した通り、応用問題は基本的な解き方の組み合わせで解けるので、学校レベルの問題を解くことがレベルアップには最適なのです。
プリントで対策
ネットで図形問題のプリントをダウンロードするのも良いでしょう。ただし、学年やレベルを考えないと、難し過ぎて役に立たない可能性があるので注意が必要です。
以下のサイトなら基本レベルのプリントをダウンロードすることができます。
- すきるまドリル
- ドリルズ
すきるまドリルでは、プリントが学年別・単元別にまとめられているので、お目当てのプリントがすぐに見つかるでしょう。
ドリルズではキーワード検索ができるので、欲しい問題をピンポイントで探すことが可能です。また問題数も豊富なので、量をこなしたいという場合にもおすすめできます。
中学入試レベルの問題を解けるサイト
発展的な問題にも挑戦させたいという方もいるでしょう。それなら「算数星人のWEB問題集」というサイトがおすすめです。
このサイトでは中学受験レベルの算数問題を無料で閲覧することができます。図形問題の最終仕上げを行うのには最適です。
中には算数オリンピックで出題された面白い問題もあるため、挑戦のつもりで気軽に取り組んで見ましょう。
市販の教材なら天才ドリル
基本的には学校の教材で勉強していれば十分ですが、必要に応じて市販の教材を購入するのも良いでしょう。
市販の教材なら「天才ドリル 立体図形が得意になる点描画【小学校全学年用 算数】」をおすすめします。これは見本を見ながら立体を書き写すだけで図形が得意になるという不思議なテキストです。
図形問題が苦手な子供は歪んだ立体を書くことが多いという事実に立脚したこのドリルでは、点と点を結ぶ点描写によって綺麗な立体を作図することを目指します。
綺麗な立体を要領よく書けるようになれば、頭の中で図形をイメージしやすくなるため、図形問題も得意になるのです。
このドリルは立体図形が苦手な子供に向けて作成されているので、図形に慣れる段階で利用するのも良いでしょう。
算数が得意になるタブレット教材も
通信教育のテキストは学校の教科書よりも分かりやすく作られているため、算数が苦手な子供にはおすすめできます。
また動画でも解説が受けられるので、苦手な分野を初歩的な内容から復習するには最適です。通信教育の教材は子供一人で進められるように設計されているため、忙しくて子供のサポートができないという場合にもおすすめできます。
さらに算数に特化したタブレット教材を提供する通信教育を利用すれば、算数を得意科目にすることも可能です。
通信教育なら費用もリーズナブルなので、出費をできるだけ抑えたいという方にも向いています。
以下の記事では算数の力も伸ばせる通信教育も紹介しています。
小学生の算数・図形問題の克服法まとめ
小学生の算数・図形問題の克服法まとめ
- 基本的な問題を数多く解く
- 複数のアプローチを持っておく
- ドリルや通信教育の活用もおすすめ
小学生の算数・図形問題の克服法について解説しました。
図形問題が苦手な小学生の場合、まずは身近なものの図形を考えることから始めると良いでしょう。また自分で作図をしてみるのもおすすめです。
そうした方法である程度図形に慣れたら、基本的な問題を数多くこなして、解法のパターンを体得させましょう。
応用問題にも基本的な解き方の組み合わせで対処できるので、中学受験を目指す場合でも基礎的な問題から練習を始めるべきです。
また通信教育を活用すれば、算数を得意科目にできる可能性もあります。
以上の内容を参考に、親子で図形問題の克服を目指しましょう。








