【中学受験】鶴亀算とは?解き方やわかりやすい教え方・小学生におすすめの問題集も紹介
「鶴亀算って何?」
「鶴亀算の解き方、教え方は?」
急に飛んでくるお子様からの質問にドキッとする保護者の方はいらっしゃいませんか?
鶴亀算の解き方を教えてあげたいけど、やり方も教え方も忘れてしまったということも少なくないですよね。
そんな保護者の方々を救うべく、今回は鶴亀算の概要から、わかりやすい解き方・具体的な問題の例までをこのページでご紹介します!
鶴亀算についてざっくり説明すると
- 小学生で学ぶ特殊算のうちの1つ
- 2種類のものの合計数から答えを導く問題
- わかりやすい解き方は大きく2つある
小学生の算数の単元である鶴亀算とは?
 まずは鶴亀算の概要から詳しく説明していきます。
まずは鶴亀算の概要から詳しく説明していきます。
鶴亀算って何?
鶴亀算とは、鶴と亀の合計の数とその足の総数から、鶴と亀それぞれの数を求める問題です。
解いていく際には、鶴の足は2本、亀の足は4本と言う条件の下、計算していきます。
例えば、「鶴と亀が合わせて5いて、足の合計数は14本です。この時、鶴と亀はそれぞれ何羽、何匹ずついますか」
といった問題があります。この場合の答えは鶴3羽、亀2匹となります。
この答えを導き出す方法を鶴亀算とよび、特殊算として教えられています。
小学4年生の段階で教えられる計算方法で、中学校で学ぶ連立方程式の基礎となる考え方が身に付く計算法です。
とは言っても、ここでは連立方程式そのものを学ぶわけではありません。その基盤となるxとyの関係性を理解することが重要視されます。
鶴と亀が出てこない問題もある
鶴亀算とはいうものの、必ずしも鶴と亀が登場し、その頭数を調べるわけではありません。他にも様々な問題の出題方法があります。
例えば、「30円のアメと80円のチョコレートが合わせて12個あり、その合計金額は660円です。アメとチョコの個数はそれぞれ幾つでしょう。」
と言ったものや
「外周1000m池があります。最初は分速200mで走り、残りは分速100mで歩いたところ、合計で7分かかりました。走った時間と歩いた時間はそれぞれ何分間ずつでしょう。」
と言う問題もあります。 つまり、2種類のものの合計がわかっている場合には鶴亀算の解き方が使えることになります。
鶴亀算の解き方は2つある!
鶴亀算に必要なのは表で考える方法と、面積で考える方法の主に2つの考え方です。
それぞれの問題に合わせて、2種類ある考え方のうちの1つを使いながら解いていく必要があります。
表を用いる考え方は鶴亀算を最初に習得するときに使うとわかりやすいのですが、要領がわかってくると面積を用いて解く方法が王道です。
また、鶴亀算の問題は方程式で解くことができるものであることがほとんどですが、ここで注意しなければいけないポイントがあります。
中学受験で出題される鶴亀算は方程式を使わずに解かせる問題ばかりであるということです。 鶴亀算と中学受験の関わりについて、次の章で詳しく見ていきましょう。
鶴亀算は中学受験で頻出
鶴亀算は小学校や通っている塾などによって、扱う場合と扱わない場合があります。いずれ中学校で習う連立方程式があれば鶴亀算は必要がないため、やらなくても良いだろうという考え方なのでしょう。
しかし、そんな鶴亀算は中学受験では超頻出問題です。
鶴亀算が得意であれば中学受験でも一歩リードできるので、受験を考えている場合は是非ともマスターしておきたい単元のうちの1つだと言えます。
また、中学受験をしない場合でも、鶴亀算を解くことは思考力を鍛える良い訓練になるので、一度チャレンジしてみることをおすすめします。
SPI試験にも登場
鶴亀算は就活の際に使われるSPI試験に登場することもあります。
しかし、この場合は考え方を見られているわけではないため、中学生以降であれば鶴亀算は連立方程式を組むことで簡単に解いてしまって構いません。小学生の時のように表や面積を使った解き方をする必要はないです。
小学生への鶴亀算の教え方は?
 この章では鶴亀算の解き方について、具体的な例を扱いながら解説していきます。
この章では鶴亀算の解き方について、具体的な例を扱いながら解説していきます。
初めは表を使って全部鶴か亀にする
「鶴と亀の合計が12で、足の合計が40であるとき、鶴と亀はそれそれ何羽、何匹でしょう」という問題を、表を使って解いてみましょう。
まず、12羽全て鶴だった場合の足の本数を算出し、その後、亀を1匹ずつ増やして足の合計本数の変化を見ます。
| 鶴 | 亀 | 足の合計 |
|---|---|---|
| 12 | 0 | 24 |
| 11 | 1 | 26 |
| 10 | 2 | 28 |
| 9 | 3 | 30 |
| 8 | 4 | 32 |
| 7 | 5 | 34 |
| 6 | 6 | 36 |
| 5 | 7 | 38 |
| 4 | 8 | 40 |
このとき、鶴が減るにつれて足の合計が2ずつ増えていくことがポイントとなり、鶴が12匹の時、16本足りないから16÷2で亀が8匹増えることになります。
合計や頭数が多すぎるときは表で全て書くことはできないため、表を使って解くときのポイントは法則を見つけることです。
この法則さえ見つけることができれば、最初から表を全て書く必要がなくなりますね!
面積を使うのがわかりやすい解き方
次に、面積を使った方法で考えてみましょう。
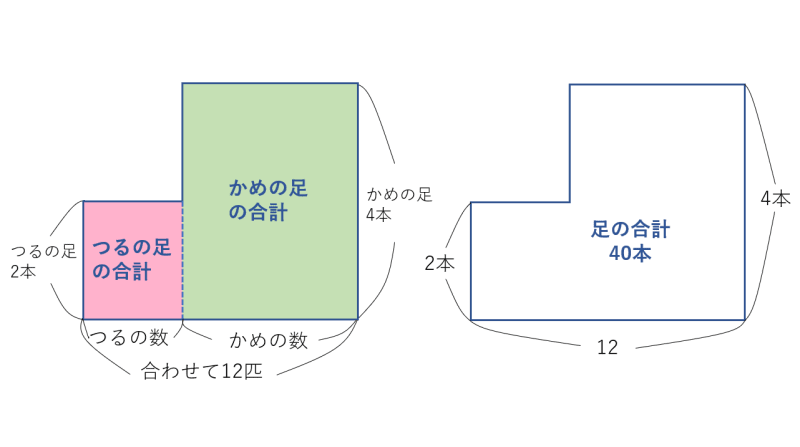
そもそも面積を使うという意味がわからないという方も少なくないでしょう。 実は、面積を使うと言っても、本当に面積を計算して使うわけではありません。
これは図を書くことで、視覚的に問題を理解する解き方のことを指します。
まず12匹全部が亀(足の本数が多い方)であると仮定し、そのときの面積(横軸は頭数、縦軸が足の数)を求めます。
このとき、(亀の数)×(亀1匹の足の数)つまり12×4で合計の足の数は48本になります。

問題になっている合計の足の数は40本であるため、12匹全てが亀だと足が8本多くなってしまいます。鶴と亀の足の数の差は(4−2)で2本であるので、8÷2で亀4匹を鶴に変えます。
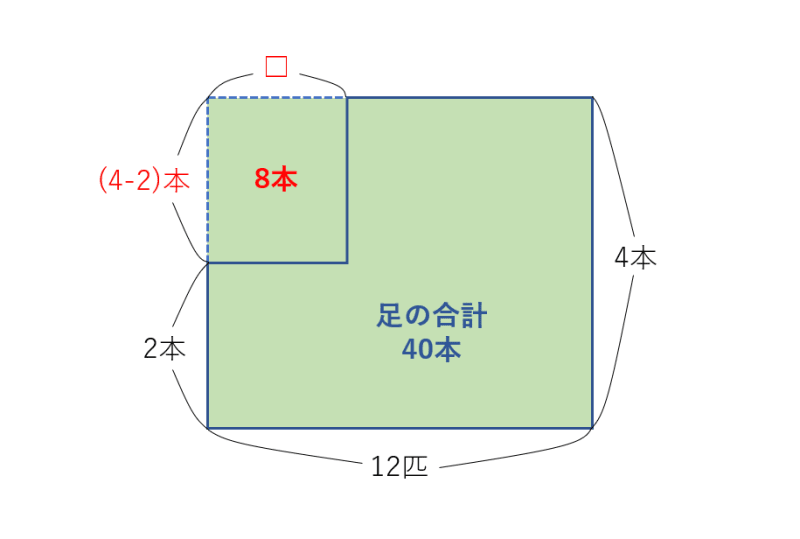
すると、鶴と亀の総数と足の本数が問題で提示されているものと一致します。
このようにして、求める方法が鶴亀算の図を使って求める考え方です。
公式も存在する!
そんな鶴亀算ですが、一応公式も存在するのです。
例題に対する公式は以下のような形になります。
鶴の数=(合計の頭数×4ー足の合計)÷(亀1匹の足の数ー鶴1羽の足の数)
鶴の数=(12×4ー40)÷(4ー2)
鶴の数=4
つまり鶴4羽、亀8匹となります。
これも考え方としては、全てが亀だった場合の足の本数と実際の足の本数の差を求めて答えを出す、と言う流れの式です。
しかし、公式を使う場合は、公式の意味、問題の意図を理解して使わなければ何をどこに当てはめたらいいのかわからなくなってしまうため、非常に間違えやすくなります。そのため、鶴亀算の根本をしっかりわかっていない、不安があるという方にはおすすめしません。
方程式で解くのは禁止?
鶴亀算で出題されるような内容の問題は、方程式で解くことが多いです。
しかし、小学生は方程式のやり方を学習しません。それゆえに方程式を使ってはいけない雰囲気があります。
子供のうちからxやyを使うより、鶴や亀など身近な考えやすい物を題材にした方がいいと言う意見もあり、少なくともすぐに方程式が小学生に導入されることはないと推測されます。とは言っても、実際に中学入試などでかなりの高レベルな問題を解く生徒がいることを考えると、これはあまり意味がなさそうな議論ですね。
つまり、方程式で解くことは禁止されているわけではありません。ただ、問題文で方程式を使わないようにという指示がある問題もあるので、上記で説明した考え方を理解しているに越したことはなさそうです。
小学生向けつるかめ算の練習問題3選!

買い物で鶴亀算
太郎君は1箱200円のお菓子と、1本100円のジュースを全部で30個買いました。レジで5000円出したところ、800円のおつりが返ってきました。
この時、太郎君は何本のジュースを買ったでしょう?
「買い物で鶴亀算」の答え
買い物の合計金額は5000-800=4200(円)。
200円のお菓子を30個買ったとすると、6000円になるので、実際の金額よりも6000-4200=1800円分高くなってしまう。
お菓子とジュースの差額は100円なので、ジュースの本数は1800÷100=18本。
買い物で鶴亀算(応用編)
運動会のために赤玉と白玉と黄玉を全部で19個購入し、値段は2160円になった。赤玉の値段は150円、白玉は120円、黄玉は50円だった。なお、黄玉は白玉の2倍の個数を買った。
この時、買った白玉の個数を求めなさい。
「買い物で鶴亀算(応用編)」の答え
表を作成すると、次のようになる。
| 赤玉 | 白玉 | 黄玉 | 合計金額 |
|---|---|---|---|
| 1 | 6 | 12 | 1470円 |
| 4 | 5 | 10 | 1700円 |
| 7 | 4 | 8 | 1930円 |
| 10 | 3 | 6 | 2160円 |
よって白玉の個数は3個。
この問題のポイントは、白玉は6個より多くはならないということです。
なぜなら黄玉の数は白玉の2倍なので、仮に白玉が7個だとすると、黄玉と白玉だけで21個になってしまい、合計の玉の個数である19個を超えてしまうからです。
あとは白玉の数を軸に表を作れば、比較的早く答えにたどり着けます。
また、この表の金額の値は等差数列になることに気づけば、最初の金額1470円と、次の金額1700円が出たタイミングですぐに答えにたどり着くことができます。
つまり、
1470+(1700-1470)×□=2160
という式から、四角に入る数字が3であるとすぐに求められます。
あとは、6-3=3より、白玉の個数は3つであることがわかります。
鶴亀算(一見すると速度算に見える問題)
太郎君は時速4.2kmで歩き、時速18kmで走る。太郎君が15分で3.35km離れた場所につくためには、何分走る必要があるでしょう?
「鶴亀算(一見すると速度算に見える問題)」の答え
まず、小数点が厄介なので、kmをmに変換する。
太郎君の歩く速さは時速4200m、走る速さは時速18000m、そして15分でたどり着く距離は3350mとなる。
次に、求めるのは「何分走るか」なので、時速を分速に直すと、
歩く速さは分速70m、走る速さは分速300mとなる。
15分間全て歩くとすると、進める距離は70×15=1050mなので、3350-1050=2300mだけ足りない。
走る時間を1分増やすごとに、進める距離は300-70=230m増える。
よって走る時間は2300÷230=10(分)。
鶴亀算の問題の対策におすすめ教材はある?

塾の教材を完璧にする
受験塾の問題集は、鶴亀算をはじめとする受験向けの問題が豊富に掲載されており、それらを完璧にすることができると合格に近づく仕様になっています。
中学受験を研究して作られた問題集がほとんどであるため、これをマスターすると大体の受験対策を網羅することができるでしょう。
そのため、考え方含め問題演習まで塾の教材をしっかりやれば十分であると言えます。むしろ1つの教材では足りないと考え、あれやこれやと様々な問題集を購入するよりも、1つの教材に絞ってそれを完璧にすることが重要です。
考え方を理解することや問題演習をすることを疎かにしてしまうと、対策不足となってしまう危険性が高まります。
受験対策問題が豊富な通信教育も!
数ある通信教育の中には中学受験に強いものもあります。そのような講座では、塾のテキストと同じように鶴亀算をはじめとする受験向けの問題が豊富に掲載されています。
塾に行っていても通信教育を補佐として使う生徒も多く存在します。
また、低学年専用の講座から提供されているため、低学年の頃から受験対策ができるところも大きな特徴です。さらに、塾に比べると低価格で受講できるため、格段にお得な受験対策をすることができるでしょう。
中学受験におすすめの通信教育はこちらの記事で紹介しています。
鶴亀算の解き方のまとめ
鶴亀算の解き方のまとめ
- わかりやすい解き方は表を使ったものと面積を使ったものの2つ
- 公式もあるけど使う時は要注意
- 鶴亀算のような問題の対策には、通信教育もおすすめ!
鶴亀算は、中学生で連立方程式を習得したあとはなかなか使うことのない計算方法です。
しかし、中学受験の対策をする際には通らざるを得ない単元 です。また連立方程式のベースとなる考え方であるため、覚えておくに越したことはないでしょう。
考え方を理解さえすれば、頭を悩ませるほど難しい問題ではないので、この機会にぜひマスターしてみてくださいね。







