【中学数学】証明問題のやり方は？解き方のコツや図形問題への対処法を解説！

数学の証明問題がわからない・できないという中学生は多いです。以下では証明問題が難しく感じる理由や解き方のコツを解説します。

中2の図形の証明が難しく感じる理由は？

中学生の数学では数多くの単元を扱いますが、ほとんどが端的に答えを求めるという性質のものです。

一方証明問題では、記述によって2つの三角形が合同であることや相似であることなどを説明します。よって数ある単元の中でも図形の証明は、異質な単元であると言えるでしょう。

独特であるということがすなわち証明問題が難しく感じられる理由です。

図形の性質を復習する

証明問題では、一方の角と他方の角が等しいことや、2辺の長さが等しいことなどを根拠にしますが、それらの根拠を見つけるためには図形の性質を理解しておかなくてはいけません。

図形の性質とは例えば、平行四辺形の対角・対辺は等しいということや、平行線の錯角は等しいということなどです。

これらが理解できていなければ証明問題を解くのは難しいので、まずはそれらをきちんと押さえてから問題に取り組むのが良いでしょう。

解き方のコツはある？

中学数学の証明問題は、解き方のパターンが数種類に限定されます。まずはこの事実を知ることが重要です。これを知るだけでも、証明問題が幾分か簡単に思えてくるでしょう。

また実際にそれらのパターンを覚えるには、問題演習を繰り返すことが一番です。

教科書や参考書を読んで解き方を覚えることも大切ですが、問題に取り組んでから解答解説を読み込む方が、効率的に解き方を体得できるでしょう。

ここからは証明問題の解き方の流れを具体的に解説します。

証明するための条件選び

合同の証明には以下3パターンの条件のいずれかを用います。

• 三組の辺がそれぞれ等しい

辺＝辺　…①

辺＝辺　…②

辺＝辺　…③

この条件を使う場合は、上記のように三組の辺がそれぞれ等しいことを例示して証明します。

• 二組の辺とその間の角がそれぞれ等しい

辺＝辺　…①

辺＝辺　…②

角＝角　…③

上記のように、二組の辺の長さとその間にできる角の大きさが等しいことをそれぞれ例示して証明します。

• 一組の辺とその両端の角がそれぞれ等しい

辺＝辺　…①

角＝角　…②

角＝角　…③

上記のように、一組の辺の長さとその両端に位置する角の大きさがそれぞれ等しいことを例示して証明します。

証明問題に取り組む際は、これらの条件のうち、どれが使えそうかという観点を持つことが大切です。

根拠を探す

上記で解説した条件を使うためには、それぞれの条件が成り立つことを明確にするための根拠を探さなければなりません。なお、根拠として使える事柄は主に以下の3つです。

1. 問題文に書かれていること（仮定）

2. 証明すべき2つの三角形で共通のこと（一つの辺を共有している場合など）

3. 図形や基本的な幾何の性質

3の「図形や基本的な幾何の性質」ですが、以下のような性質をよく用います。

• 対頂角：二直線が交わってできる向かい合った角は必ず等しい
• 平行線の錯角・同位角：平行なら錯角・同位角は必ず等しい
• 図形の性質：平行四辺形や正三角形など図形が持つ性質

たいていの場合、1〜3のいずれか（もしくは全部）から条件を説明するための根拠が見つけられるはずです。

テンプレートに当てはめる

中学数学における証明問題は、合同の証明以外にもありますが、解答の流れはワンパターンです。そのため、以下で紹介する合同の証明をテンプレートにすると良いでしょう。

例題

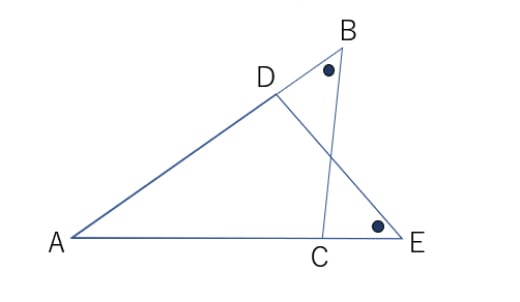
図において、AB=AE、∠ABC=∠AEDの時、△ABC≡△AEDとなることを証明します。

△ABCと△AEDにおいて、

仮定から、

AB=AE …①

∠ABC=∠AED …②

共通だから、

∠BAC=∠DAE …③

①、②、③より

一組の辺とその両端の角がそれぞれ等しいから、

△ABC≡△AEDである。

中学数学で扱われる難問3選に興味がある方は、以下の記事を参考にしてください。

証明問題はパターンが少ないので、慣れれば実は簡単です。

覚えておくべき条件が少ない！

中学数学の証明問題をクリアするには、合同な三角形の性質以外に以下の性質・条件を覚えておけば十分です。

• 平行線の性質
• 平行四辺形になる条件
• 直角三角形の合同条件
• 二等辺三角形の性質

頻出の証明問題で用いる性質・条件はこのくらいなので、覚えるのはそれほど難しくないでしょう。

これらさえ覚えれば、あとは証明に必要な条件を満たすように根拠を探し、先述したテンプレートに当てはめるだけなので、慣れれば実に簡単です。

よって証明問題をそこまで難しく捉える必要はないでしょう。

覚えるべき条件・性質をチェック

以下では、証明問題をクリアするのに必要となる条件・性質（合同な三角形の性質以外）を紹介します。

＜平行線の性質＞

• 2直線が平行なら、同位角は等しい
• 2直線が平行なら、錯角は等しい

＜平行四辺形になる条件＞

• 2組の対辺がそれぞれ平行
• 2組の対辺の長さがそれぞれ等しい
• 2組の対角がそれぞれ等しい
• 対角線がそれぞれの中点で交わる
• 1組の対辺が平行で、その長さが等しい

＜直角三角形の合同条件＞

• 斜辺と1つの鋭角がそれぞれ等しい
• 斜辺とその他の1辺がそれぞれ等しい

＜二等辺三角形の性質＞

• 二等辺三角形の2つの底角は等しい
• 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する
• 二辺の長さが等しい三角形は二等辺三角形

角度問題より実は簡単？

角度問題も証明問題と同様、多くの中学生が苦手とする単元です。角度問題も問題の形式に慣れればできるようになりますが、やはり基本的なルールはきちんと押さえなければいけません。

よって両者は似ていますが、難易度としては証明問題よりも角度問題の方が高いでしょう。なぜなら、角度問題を解くには図形の性質を複数用いなければならないからです。

これに対し、証明問題なら一つの条件さえ理解していれば解くことができます。証明問題は記述をしないといけないのでハードルが高いように見えますが、内容としては実に簡単です。

角度問題に用いる性質

角度問題では以下のような性質を用います。

1. 対頂角

2. 平行線の同位角・錯角

3. 三角形の内角・外角

4. 多角形の内角・外角

3と4に関しては以下で解説しておきましょう。

＜三角形の内角・外角＞

• 三角形の内角の和は180度
• 三角形の外角は、それととなり合わない2つの内角の和に等しい

＜多角形の内角・外角＞

• n角形の内角の和は180度×(n-2)
• 多角形の外角の和は360度

通信教育でつまずきを克服

冒頭でも述べた通り、証明問題は中学数学で扱う単元の中でも「異質」なので、初見だと難しく見えることが多いです。

しかし、実際はテンプレートに当てはめるだけなので、全然難しくありません。そのため、きちんと予習をしておけば、学校の授業に遅れる心配もないでしょう。

なお、証明問題の予習をするなら通信教育を活用するのがおすすめです。スムーズに問題が解けるように誘導してもらえるため、誰でも難なく証明問題をクリアできるでしょう。

タブレット学習と相性抜群

タブレット教材なら、図形のアニメーションを動かしたりして視覚的に性質などを理解することができるため、証明問題の勉強には最適です。

しかし、証明問題ができるようになるには、実際に手を動かして記述の仕方を体得する必要もあります。

よってタブレット教材で基礎を学びつつ、紙教材を用いた演習で記述力も鍛えられるような通信教育を選ぶのが特におすすめです。

中学数学の証明問題のやり方について解説しました。

証明問題は一見難しいように思われますが、慣れれば実に簡単です。解き方のパターンは決まっているので、そのことを理解するだけでも幾分か簡単に思われてくるでしょう。

勉強の仕方としては、まずは図形の性質と解き方のテンプレートを覚え、その後は問題演習をひたすら繰り返すだけです。形式にさえ慣れれば問題なく解けるようになるでしょう。

しかし、証明問題は中学数学の単元の中でも「異質」なので、初見では難しく感じられることも事実です。そのため、タブレット教材などを活用して予習・復習をするのも効果的でしょう。

以上を参考に、早速証明問題を勉強してみましょう。