中学生の数学の公式一覧！図形の定理から解の公式まで学年別に分かりやすく解説！

中学生の数学では、小学校の算数のように日常生活で役立つ公式が数多く登場するわけではありません。

しかし、中学生の数学で習う公式は、いずれも高校数学の土台となる重要なものばかりです。数はそれほど多くないので、復習をきちんとして全て完璧に覚えてしまうのが良いでしょう。

中学生数学の公式は中1単元から多く存在

中学生の数学では、中1の段階から重要な単元が数多く登場します。中でも方程式や関数、平面図形、空間図形などの単元には覚えるべき公式が多いです。

それらの単元及び公式は、中2・中3や高校の数学で学ぶ内容にも応用されるので、確実に身に付けておかなければなりません。

中1での学習が不足していれば、学年が上がった時につまずく原因となってしまうので、中1で習う公式については中1のうちにマスターすることを心がけましょう。

また中2・中3で数学が苦手になってしまった場合は、中1の基礎ができていない可能性があるので、必要に応じて中1の内容を見直すのがおすすめです。

計算速度を上げるのに便利

中学や高校で習う公式は、小学校の算数で習う公式よりも実生活との関連が薄い内容のものが多いです。

そのため、なかなか覚える気にならなかったり、具体的なイメージがしにくいことから覚えるのが難しいと感じることもあるでしょう。

しかし、公式を覚えることによって計算の速度を上げることができるため、テストで良い点を取るには公式の暗記が欠かせません。

また中学生で習う公式は高校数学で習う単元に基礎にもなるので、大学受験で成功するためにもきちんと覚えておく必要があります。

なお、実生活との関連の薄いものは丸暗記しにくいので、覚えにくい場合は「どうしてそうなるのか」を把握し、理解をベースに覚えるのが良いでしょう。

ここからは中学数学に登場する公式を一気に紹介します。

計算公式

まず「ルートの有理化」は必ず使えるようにしておきましょう。

「1/√3=1×√3/√3×√3=√3/3」のように、分母のルートを分母・分子にルートをかけることによって消す公式です。

また以下4つの乗法公式も覚えておくべきです。

• (x+a)(x+b)=x^2+(a+b)x+ab
• (a+b)(a-b)=a^2-b^2
• (a+b)^2=a^2+2ab+b^2
• (a-b)^2=a^2-2ab+b^2

なお、「x^2」は「xの2乗」を意味します。

解の公式

二次方程式ax^2+bx+c=0の解が、「x={-b±√(b^2-4ac)}/2a」になるという公式です。

例えば、「x^2+4x+1=0」という式の解をこの公式を使って求めるなら、「x={4±√(4^2-4×1×1)}/2×1」になり、答えは「x=-2±√3」となります。

関数

関数に関しては以下4つの公式を覚えておくべきです。

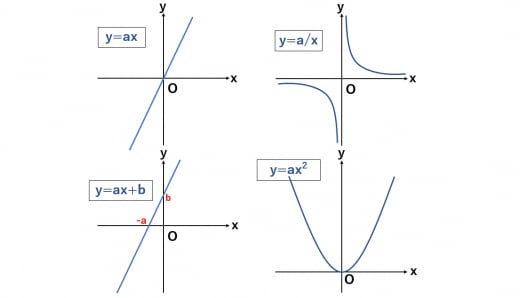
• 比例：y=ax
• 反比例：y=a/x
• 一次関数：y=ax+b
• yがxの2乗に比例する関数：y=ax^2

下図はa>0,b>0の場合。

なお、一次関数に関しては以下のようなバリエーションがあります。

• 傾き・切片が与えられる
• 傾きと点が与えられる
• 変化の割合と点が与えられる
• 切片と点が与えられる
• 2点が与えられる
• 点と平行になる直線が与えられる

これらに対応するにはy=ax+bのaが傾き（変化の割合）、bが切片になることを覚えておかなくてはなりません。

また「変化の割合=yの増加量/xの増加量」という公式も必要です。

さらに関数y=ax^2について、xの値がαからβまで増加するなら「変化の割合=a(α+β)」という公式もあります。

円・おうぎ

円・おうぎの単元では、以下4つの公式が必須です。なお、rは円・おうぎの半径、aはおうぎの中心角を表すとします。

• 円の面積：πr^2
• 円周の長さ：2πr
• おうぎ形の面積：πr^2×a/360
• おうぎ形の弧の長さ：2πr×a/360

体積

柱体及び錐体の公式は以下の通りです。なお、柱体には円柱・四角柱（直方体・立方体など）・三角柱、錐体には円錐・四角錐・三角錐がそれぞれ含まれます。

• 柱体の体積：(体積)=(底面積)×(高さ)
• 錐体の体積：(体積)=(底面積)×(高さ)×1/3

円錐

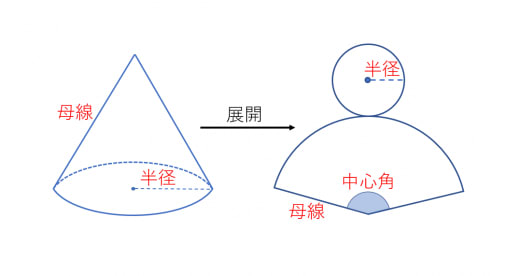
円錐に関しては以下2つの公式も合わせて覚えておきましょう。

• 円錐の中心角：半径/母線×360
• 円錐の側面積：母線×半径×π

なお、側面積は「π×半径^2×中心角/360」で求めることもできます。

球

球に関する公式は以下の二つです。

• 球の表面積：4πr^2
• 球の体積：4/3πr^3

なお、両者は混同しやすいので、表面積の公式は「表面は心配あるある」、体積の公式は「身の上に心配あーるの三乗」という語呂合わせを使って覚えるのが良いでしょう。

二等辺三角形

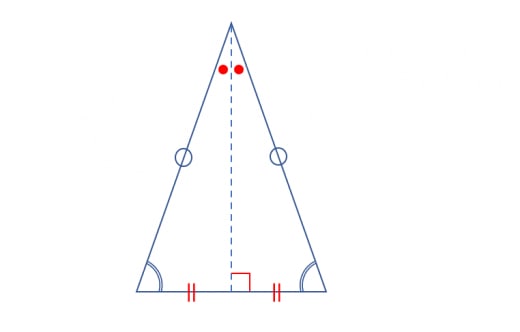
二等辺三角形とは、2辺が等しい三角形のことを指します。二等辺三角形に関しては以下2つの性質を覚えておくと良いでしょう。

• 底角が等しい
• 頂角の二等分する線分は底辺を垂直に二等分する

また「2辺が等しい」もしくは「2つの角が等しい」という条件を持つ三角形は二等辺三角形になるということも合わせて覚えておくべきです。

合同・相似条件

以下では合同条件・相似条件を紹介します。

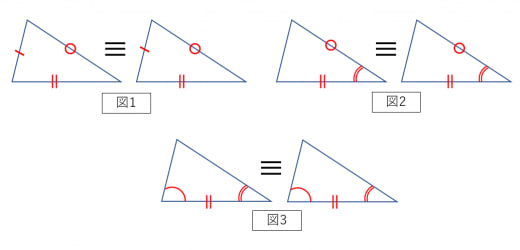
＜三角形の合同条件＞

• 3辺がそれぞれ等しい（下図1）
• 2辺とその間の角が等しい（下図2）
• 1辺とその両端の角が等しい（下図3）

＜直角三角形の合同条件＞

• 斜辺とその他の1辺が等しい（下図1）
• 斜辺と1つの鋭角が等しい（下図2）

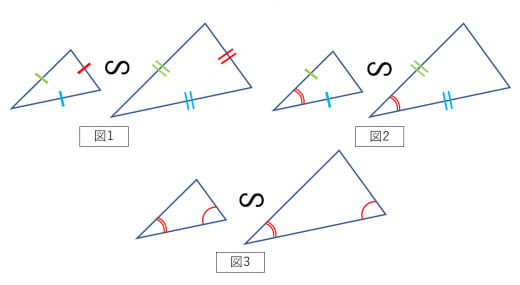
＜三角形の相似条件＞

• 3辺の比がそれぞれ等しい（下図1）
• 2辺の比とその間の角が等しい（下図2）
• 2組の角が等しい（下図3）

図形の性質

正三角形と平行四辺形の性質はそれぞれ以下の通りです。

＜正三角形の性質＞

• 3辺が全て等しい（定義）
• 3つの角が全て60度

＜平行四辺形の性質＞

• 2組の対辺がそれぞれ平行（定義）
• 2組の対辺がどちらも等しい
• 2組の対角がどちらも等しい
• 対角線がそれぞれの中点で交差
• 1組の対辺が平行かつその長さが等しい

なお、上記は平行四辺形になるための条件でもあります。

また長方形・ひし形・正方形も平行四辺形の一種ですが、それぞれの定義は以下の通りです。

• 長方形：4つの角が全て直角な四角形
• ひし形：4つの辺が全て等しい四角形
• 正方形：4つの角が全て直角かつ4つの辺が全て等しい四角形

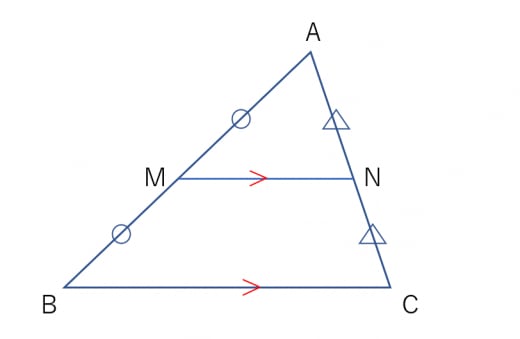
中点連結定理

△ABCに関する中点連結定理は以下の2つです。

• MN//BC
• MN=1/2BC

つまり2辺の中点同士を結んだ線分は底辺と平行になり、長さは底辺の半分になるということです。中学数学の図形問題で中点が出てきたら必ずと言って良いほどこの定理を使うので、きちんと覚えておきましょう。

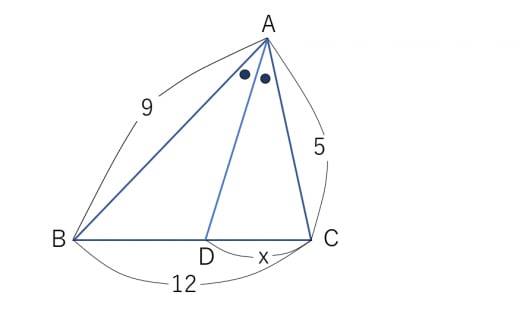
角の二等分線

△ABCにおける角BACの二等分線と線分BCの交点をDとすると、「AB:AC=BD:DC」という等式が成り立ちます。それが角の二等分線の性質です。

例えばABが9、ACが5、BCが12の時、DCの長さは幾らかという問題があったとします。DCをxとすれば、「9：5=12-x：x」という式が成り立つため、答えは30/7です。

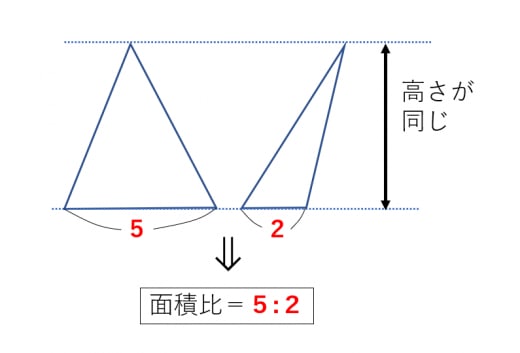
面積・体積の比

2つの図形を比べる場合、面積と体積には以下のような関係が成り立ちます。

＜両者は相似（相似比a：b）＞

• 面積比はa^2：b^2
• 体積比はa^3：b^3

＜両者は高さが同じ三角形＞

• 底辺の比=面積比

円周角の定理

円周角の定理は以下の6つです。

• 同じ弧に対する円周角は等しい（下図1）
• 同じ弧に対する中心角は円周角の2倍（下図2）
• 弧の長さが同じなら円周角・中心角も等しい（下図3）
• 円周角・中心角の大きさは弧の長さに比例（下図4）
• 直径に対する円周角は90度になる（下図5）
• 円に内接する四角形の対角の和は180度になる（下図6）

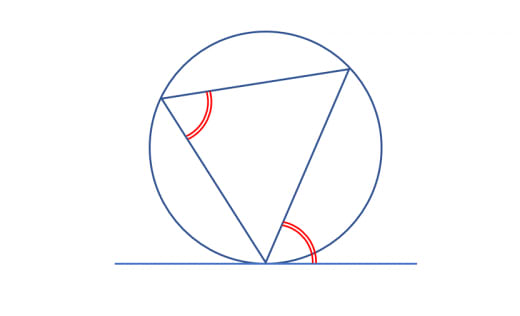
接弦定理

円の接線と接点を一端とする弦が作る角は、その弦を挟んで反対側にできる円周角の大きさに等しいというのが接弦定理です。

円と円に内接する三角形、接線が出てきた時は接弦定理を使うことを検討するのが良いでしょう。

なお、接弦定理は接線と弦でできる角が90度より大きい時にも成り立ちます。

三平方の定理

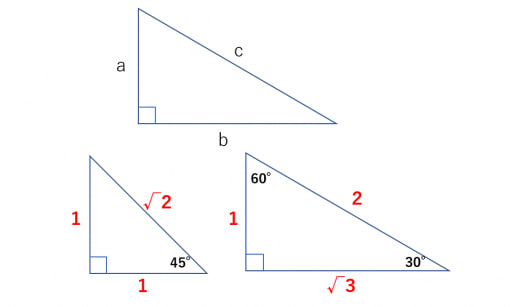
三平方の定理（a^2+b^2=c^2）は、直角三角形の斜辺の2乗は、その他2辺の2乗の和になるという定理です。

またこの定理の応用として、以下の2つも覚えておくと良いでしょう。

• 直角二等辺三角形の辺の比は1：1：√2
• 60度と30度の角を持つ直角三角形の辺の比は1：√3：2

ここからは多くの中学生が苦手とする頻出分野について解説します。上記で紹介した公式とも関連するので参考にしてください。

証明問題

図形の証明問題は中学生も最もつまずきやすい分野と言っても過言ではありません。

まずは上記で解説した「合同・相似条件」や「図形の性質」などをきちんと覚えるのが良いでしょう。

またそれらに加えて、以下の内容も押さえておく必要があります。

• 仮定：問題文に書いてあることは正しいと仮定して使って良い
• 共通：同じ辺や角を共有している時は、それらに関しては必ず等しい
• 対頂角：二直線が交わってできる向かい合った角は必ず等しい
• 錯角・同位角：平行なら錯角・同位角は必ず等しい

なお、中学数学の証明問題のパターンは決まっており、根拠の使い方や証明の流れも大体同じなので、問題演習をこなして解法を覚えることが大切です。

関数（中2・中3）

中2・中3の関数も非常につまずきやすい単元です。まず中2の一次関数ですが、ここでつまずく場合は連立方程式や中1で扱う文字式の理解が不十分である可能性があります。

そのため、xやyの使い方がよく分かっていないような場合は、中1の内容から遡って復習するが良いでしょう。

また中3の二次関数でつまずく場合は、一次関数が理解できていない可能性があるので、一次関数の復習から始めるべきです。

角度の問題（中2）

角度の問題でつまずく生徒も多いですが、これに関してはある程度慣れることで苦手を解消できるでしょう。

また問題演習に取り組む前に、三角形の外角は二つの内角の和にあることなど、基本的なルールを確認することもおすすめです。

原理や公式が理解・暗記できていないことが苦手の原因であるため、まずはそれらをしっかりインプットすることから始めるのが良いでしょう。

公式は教科書の解説を読んで、問題演習を解くという流れで基本的には暗記することができるはずです。

しかし、教科書は復習には不便だと感じたり、問題演習の量が物足りないと思われることもあるでしょう。

そうした場合は、以下で紹介するような教材を使うのがおすすめです。

公式暗記向けのアプリを使う

公式を手軽に確認したい場合は、スマホアプリを使うのも良いでしょう。スマホアプリならスキマ時間を使って復習ができるので、忙しい中学生にはぴったりです。

例えば、「数学公式集」というアプリなら中学や高校で習う公式や定理などを簡単に確認することができます。

また頻繁に使う公式や覚えにくい公式などをお気に入り登録することができるので、問題演習や暗記学習の際に便利です。

スマホアプリを使った数学の学習法やおすすめのアプリに関して知りたい方は、以下の記事を参考にしてください。

通信教育でつまずきを克服

中学数学でつまずいてしまった場合は、通信教育を利用して苦手を克服するのがおすすめです。

なお、通信教育なら公式の暗記だけでなく、学校の予習・復習や高校受験対策もできます。

おすすめはタブレットで学べる教材

数学に苦手意識がある中学生には特にタブレット教材がおすすめです。ゲーム感覚で楽しく手軽に勉強できるので、継続しやすくなっています。

またタブレットであれば図形などのイラストやアニメーションを見ながら公式を勉強できるので、教科書よりも理解・暗記が捗るでしょう。

タブレット教材のみだと不安だという方は、紙教材や添削指導もついている通信教育も検討してみましょう。

中学生におすすめのタブレット教材は是非以下の記事でチェックしてみてください。

中学生の数学で習う公式一覧を紹介しました。

なお、公式の暗記ですが、教科書の解説をよく読んで練習問題を解けば、基本的には覚えられます。

また「数学公式集」というスマホアプリを補助教材として利用するのもおすすめです。

さらに数学が苦手ならタブレット教材を活用するのも良いでしょう。図形などのイラストやアニメーションが見られるので、教科書よりも公式が覚えやすいはずです。

以上を参考に、今回紹介した公式をしっかり暗記しましょう。