【例題あり】旅人算とは?出会い算・追いつき算など種類別の解き方や教え方のコツも解説
更新
「旅人算って一体何?」
「解き方を子供に教えたいけどやり方がわからなくて……」
こんな疑問をお持ちの方もいるのではないでしょうか?
旅人算は、中学受験の算数で必要になる単元です。かなり特殊な内容で大人でも理解が難しいため、子供に質問された時に苦労する親御さんも多いことでしょう。
そこでこの記事では旅人算の基本はもちろん、応用問題についても、それぞれの考え方や解き方、教え方を例題を交えながらご紹介していきます。
一度理解してしまえばそこまで難しいものでもありませんので、ぜひ最後まで読んで参考にしてください。
旅人算の解き方や教え方についてざっくり説明すると
- 旅人算は「出会い算」「追いつき算」と2種類に分別できる
- 公式はある程度決まっているが、頭に入るまでは線分図を利用すると良い
- 単位変換も問題の中に組み込まれていることが多いため、単位の知識も必要
そもそも旅人算とは

旅人算とは、小学生算数の「速さ」を土台とした文章題です。
「速さ」という概念も難しいため、それを応用した旅人算も一見解けそうにないと感じられる問題が多いです。
そのため、「算数」のカテゴリの中ではトップクラスに難易度が高い問題として知られています。
旅人算は、就活にも利用されています。大学生の能力をテストするための試験「SPI」にも出題されるため、就職活動中の大学生にとっても大きな課題とされています。
中学受験でも頻出
旅人算がよく話題に上がるのが、中学受験です。
中学受験で出題される問題は、小学校で習う単元を元にしながら、非常に発展的な内容が含まれます。その一つが旅人算です。
問題自体は「太郎くんと花子さんは同時に家を出ましたが……」のように可愛らしい物語風になっているので、文章を読むだけだと簡単そうに見えます。
しかし解こうとすると非常に難しく、多くの子供たちを悩ませる難問となっています。
文章構成はそこまで難しくないものの数字があちこちに出てくるため、日本語と数値、両方ともしっかり理解できないと正答に辿りつけません。こうしたことも、混乱しやすい原因の一つと言われています。
旅人算の種類と例題

旅人算という単元は、大きく分けて「出会い算」「追いつき算」と、2種類に分別されます。
他にも「追いかけ算」「速度算」など細かく分類されることもあるのですが、追いかけ算や速度算などは上記の2種類のどちらかと同じものだと考えるのが一般的です。
出会い算と追いつき算の区別は、2つの物体(もしくは人物)の動く方向によって決まります。
それぞれの内容を詳しくご紹介して行きましょう。
出会い算
出会い算は、2つの物や人が向かい合って進み、出会うまでの時間や距離などを算出する問題です。
よく利用される公式は以下のとおりです。
- 出会うまでの時間=2点間の距離÷速さの和
2者の距離をお互いに同時に縮めていくと考えると、イメージしやすいでしょう。
紙の上で図を書くだけでは理解できない場合は、人形などを使って、互いに違うスピードで近付いていくことを実際にやってみると、感覚がつかみやすいです。
実際の図や例題は以下のようになります。
問題
A地点とB地点は1200m離れています。タイ子さんはA地点から毎分40mで、学君はB地点から毎分60mで歩いています。2人が出会うのは何分後ですか。
先程説明した公式を使って解いてみましょう。
解説・解答
(解説)
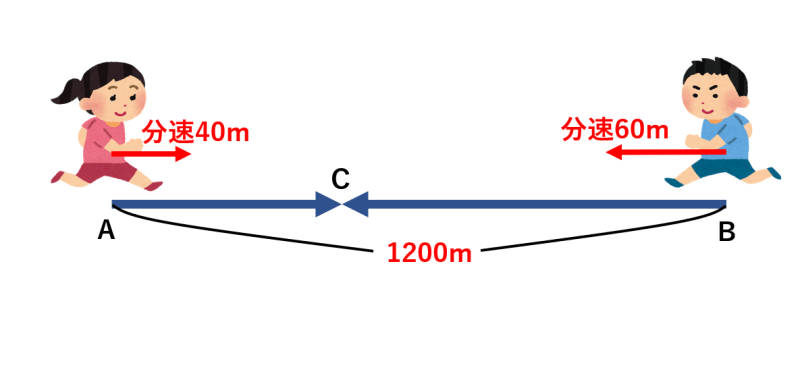
2人が歩く道のりの合計は1200mです。
2人の移動する速さの合計は
60m/分+40m/分=100m/分
です。つまり二人合わせて毎分100mずつ進むことがわかります。
つまり、2人が出会うまでの時間は、
1200m÷100m/分=12分
と計算できます。
(解答)12分
追いつき算
追いつき算は出会い算とは逆に、離れた位置にいる2者が同じ方向に動いていき、前にいるほうに後ろが追い付くまでの時間や距離を算出する問題です。
公式は以下のようになります。
- 追いつくまでの時間 = はじめの距離 ÷ 速さの差
追いつき算の問題は、2者が同時にスタートする場合もあれば、一方がある程度進んだ後にもう一方が進み始めるという問題もあります。
こちらも出会い算と同じように、実際に教える時は人形などを使って説明したほうがわかりやすいでしょう。
よく出される例題は以下のようになります。
問題
学君は毎分40mで山に向かって歩いています。タイ子さんは学君の忘れ物に気が付き、追いかけました。
タイ子さんが追いかけ始めた時点で、学君とタイ子さんの距離は1200mありました。タイ子さんは毎分60mで走っています。
タイ子さんが学君に追いつくのは、タイ子さんが出発してから何分後ですか。
上記の公式を利用して解いてみてください。
解説・解答
(解説)

2人の移動する速さの差は
60(m/分)-40(m/分)=20(m/分)
です。つまり二人の距離は毎分20mずつ縮んでいくことがわかります。
二人の距離は1200m離れていました。
つまり求める時間は
1200(m)÷20(m/分)=60分
より、60分と計算できます。
(解答) 60分
注意が必要な場合
出会い算と追いつき算は別々に出題されることも多いですが、応用問題の場合は両方の要素が絡み合った文章題が出ることもあります。
例えば、進む方向を途中で変えることで、出会い算と追いつき算両方の概念を同時に考えさせるような問題など、子供にとってはかなり難しい内容になります。
とはいえ進む方向が変わるまでは、出会い算もしくは追いつき算の方法で解けます。動きが変化する場所さえわかれば、問題を2つに分けて考えることで理解することができるでしょう。
図や例題は以下のとおりです。
問題
近藤くんと加藤くんはA地点から同時にB地点に出発します。近藤くんの歩く速さは分速60m、加藤くんが歩く速さは分速36mです。
先にB地点についた加藤くんは、時間をおかずすぐにA地点に引き返しました。
近藤くんが折り返してから30m進んだところでたかしくんとすれ違いました。
この時、二人がすれ違ったのはA地点を出発してから何分後でしょうか。
解答・解説
この問題で最も重要なポイントは、近藤くんが折り返してから30m進んでいたことから、近藤くんは加藤くんよりも「30(m)×2=60(m)」だけ多く進んでいることに気づくことです。
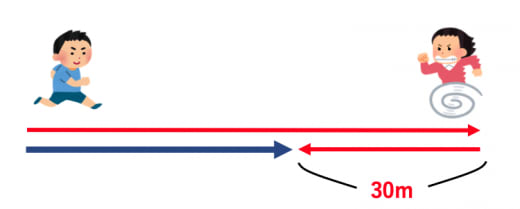
近藤くんは加藤くんよりも1分間で「60(m)-36(m)=24(m)」だけ多く進むので、求める時間は
60÷24=2.5(分)
(解答)2.5分
旅人算を解くコツと教え方のポイント

旅人算は通常の小学校の授業では深く扱わない内容のため、親御さんにとっても理解が難しいと感じられることが多いです。
親御さんがお子さんに旅人算を教えたいと思っても、苦労することもあるでしょう。
この段落では、旅人算のコツや教え方のポイントを解説します。
まずは正しく図で捉える
旅人算を解くためには、問題文の内容を図にして、正しく理解することが非常に大切です。
この時、あまりに情報を入れすぎた図を作成してしまうと、注目すべき数字を見極めることができません。あまり複雑な図は書かずに、線分図として表記するのがおすすめです。
向き・現在地・速度に注目する
旅人算派問題によって色々なシチュエーションがありますが、どの問題も以下の情報に注目すれば簡単に解けます。
- 移動する方向
- 今いる位置
- 速度
これら3つの要素がわかれば、あとは公式に当てはめて計算すれば答えが出ます。線分図を書く時にも、これらの情報を入れて作成してください。
1分または1時間あたりで考える
旅人算の問題は、登場人物(もしくは物)が複数出てきます。
最初から全ての動きを把握することは難しいですので、まずは短いスパンで考えてみると良いでしょう。
問題文に出てくる「速さ」が分速なら1分あたり、時速なら1時間あたりで、それぞれの登場人物がどのように動いていくかを把握してください。
どうしても動きがイメージできない場合は、人形、もしくは消しゴムや鉛筆を実際に動かしてみて、おおまかな動きを目で確認するとわかりやすいです。
単位のミスに気を付ける
旅人算は、問題を複雑にするために時間や分、m、kmなど、複数の単位を混ぜて出題されることがあります。
単位変換は「速さ」と同じく、苦手としている小学生が多いですので、単位変換に慣れておくことも重要です。
大人でも稀に時間と分、mとkmの関係がわかっていないことがあります。この機会にしっかり確認しておいてください。
旅人算の応用問題

旅人算の応用問題の中には、直線状で進んでいく単純な内容ではなく、複数の人物が複雑な動きをするような問題も存在します。
この場合は線分図ではなく、ダイヤグラムを利用した図形的な考察が必要になるでしょう。
具体例をご紹介します。
池の周りを回る旅人算
旅人算には「池の周りを回る」「グラウンドを走る」というように、円形の動きをする問題もあります。
円形の動きをするという内容の旅人算は一周分の距離が明示されていないことが多く、一周するのにどのくらいの時間がかかるのか、基本的な公式では求められません。
この場合は、まず速さの比を利用して、池やグラウンド一周分の長さ(距離)を求めることから始めると良いでしょう。
ただ、情報を意図的に制限して、どうしても一周分の距離が求められない問題もあります。このケースでは、速さの逆比の差と距離の差を総合して、答えを算出する必要があります。
3人旅人算
旅人算は基本的に2つの人物や物の動きを追う問題ですが、応用問題の中には「3人旅人算」も存在します。直線の上で動きが展開される場合もあれば、円形の動きをすることもあります。
このタイプの問題では、3者のうち2つずつをペアで考え、「3組の旅人算」として解くとわかりやすいでしょう。
3人旅人算は1つの問題で普通の内容の3倍以上の計算をすることになりますので、非常に難易度が高いです。そのため、難関校で出題されやすい傾向にあります。
さらなる問題演習を積みたい場合は通信教育
旅人算は、ここまでにご紹介した内容以外にも非常に多種多様な応用問題が出されます。
さらなる問題演習を積みたい方には、中学受験に特化した通信教育を受講することをおすすめします。
旅人算だけでなく「鶴亀算」など、中学受験で頻出する難問について、一通りの対策をすることができるものもあります。
詳しくは以下の記事を参考にしてください。
旅人算の解き方や教え方まとめ
旅人算の解き方や教え方まとめ
- 「出会い算」「追いつき算」ともに公式があるのでまずはしっかり理解しよう
- 単位の変換でつまずく場合は、過去の復習をして基礎を固めること
- 線分図はあまり複雑にせず、どうしてもわかりにくい時は人形などを使って動きを確認してみよう
旅人算は大人にとっても複雑な問題ですが、教える側がしっかり理解していないとお子さんには教えられませんよね。
まずは問題の内容や公式をしっかり把握して、理解を深めてください。応用問題を解きたい時は通信教育を利用するなどして、効率良く対策をしていきましょう!







