【練習問題アリ】分数の通分を習得しよう!やり方や最小公倍数を簡単に計算するコツも解説
更新
「分数の通分って何?」
「分数の通分ってどうやるんだっけ?」
自分のお子さんに分数を教えようとしたときに、「あれ?通分って何だったっけ?」と忘れていることはありませんか?
分数の仕方は覚えていても、いざ「通分」というワードが出てきたときに何のことだったか思い出せないことは多々あります。
まず、通分とはどういうものだったのかを確認していきます。
そして、通分を行うときに必要となってくるのが最小公倍数です。
最小公倍数もまたワードそのものを忘れている可能性があり、その確認をするとともにどのように最小公倍数を求めるかのコツも存在します。
通分の仕方と最小公倍数の求め方のコツ、そして通分の練習問題からオススメの教材もご紹介していきます。
分数の通分についてざっくり説明すると
- 分数の計算で突然難しく感じるのが通分
- 通分をマスターする前に約分をマスターしなければならない
- 最小公倍数を見つけることで通分が簡単になる
そもそも通分とは

分数の足し算・引き算をするうえでかかせないのが通分。
しかし、子どものころに学んだ通分という言葉が一体どんなものだったのか忘れている方は多いのではないでしょうか?
そこで、まずは「通分とは何か?」ということから見ていきたいと思います。
通分って何?
通分とは、分母が違う複数の分数の分母を統一することです。
例えば3/7と4/9ではどちらが大きいかすぐに分かりますか?
ちょっとみただけではすぐにどちらが大きいか分かりませんよね。
そこで通分を用います。
通分をすることで分母が統一されると分子を見ただけで大きさを比較できます。
また、分母がそろうことで分数の足し算や引き算をすることが可能になります。
通分の前に約分をマスターする
早速通分を用いて分数の比較や計算にチャレンジしたいところですが、その前に約分をマスターしておく必要があります。
約分とは、例えば3/6なら、上下両方を3で割って、1/2としても同じ数を表すことができます。
つまり、6個に切ったケーキの3つ分と、2つに切ったケーキの1つ分は同じ量であると言うことですね。
分数を通分する時、先に約分しておかないと、通分した後の分母が大きくなってしまって計算が面倒になることが多いです。
例えば5/14と8/35を通分するときに、約分をしないで行うと165/490と112/490となってしまい、分子の数字も非常に大きくなって計算しづらいですね。
約分をしておくことで、分数の比較がしやすくなりますし、計算もしやすくなります。
通分のやり方は?

分母をそろえることが通分ということがわかりましたね。
それではここから分母をそろえるやり方を解説していきます。
分母の最小公倍数を見つける
再び3/7と4/9の分数を用いて見ていきたいと思います。
まずは分母を最も小さい数でそろえることから始めます。
分母を最小公倍数にそろえるのですが、3/7の分母は7、4/9の分母は9ですのでそれぞれの分母の倍数を見ていきます。
7の倍数は7、14、21、28、35、42、49、56、63…
9の倍数は9、18、27、36、45、54、63、72、81…
以上のことから7と9の最小公倍数は63であることが分かります。
分母に合わせて分子の倍分をする
分母が7の分数は先ほどの最小公倍数である63に合わせますので9倍にしますが、分子も同じく9倍にします。
分母が9の分数も同じく先ほどの最小公倍数である63に合わせて7倍にし、分子も同じく7倍にします。
すると、
3/7=3×9/7×9=27/63
4/9=4×7/9×7=28/63
となり、4/9の方が大きい数であることが分かります。
通分のための最小公倍数の求め方

最小公倍数の求め方は基本的な求め方と素早く計算するコツがあります。
どちらもマスターして、通分が簡単に感じられるようにしていきましょう。
最小公倍数の基本的な求め方
倍数、というのはある数を2倍、3倍、4倍…と倍にしたら得られる数のことです。
6の倍数は
6×1=6
6×2=12
6×3=18
、、
と続いていきますので6、12、18、24、30、36、、であることが分かります。
公倍数は2つ(かそれ以上)の数字に共通の倍数、ということですから、 例えば4と6の公倍数は
4が4、8、12、16、20、24、28、、
6が6、12、18、24、30、36、、
つまり 12、24であることが分かります。
その中でも最小公倍数とは公倍数の中で最小のものを指しますので、4と6の最小公倍数は12であることが分かります。
連除法で素早く計算するコツ
この計算法では、まず公約数を求めるために2つの数字を横に並べて書き、その左側に2つの数字を共通して割ることができる小さい数字(1より大きいもの)を書きます。
その数で割ったあとの2数をしたに書く、、というのを繰り返して2つの数に共通で割れる数がなくなったとき、左に並んだ数全部と、最後に並んだ2つの数を全てかけ算をすると最小公倍数が出てきます。
このやり方を簡単な式で表しているのが連除法です。
連除法ははしご算、すだれ算と呼ばれることもあります。
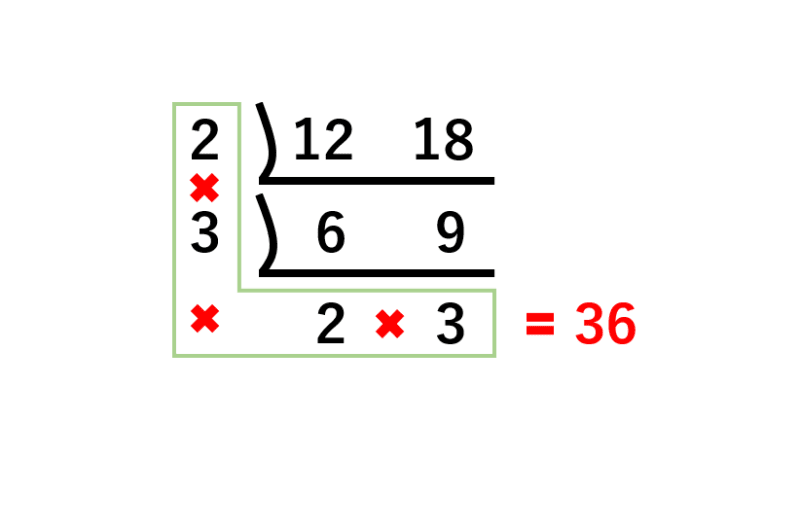
12と18で同時に割ることができる一番小さな数字は2で、12と18を2で割った数は6と9です。

6と9もまだ3で割ることが可能で、6と9を3で割った数は2と3です。

これ以上割り切れなくなった時点で最初に割った2と3、そして先ほど割り切れなくなった2と3を全てかけ算すると最小公倍数の36が出てきます。
3つ以上の数の最小公倍数
最小公倍数は最大公約数と比べると注意しなければならない点があります。
なぜなら3つ以上の数の最大公約数は2つの時と手順は同じなのですが、最小公倍数の場合は最後に出た数字3つのなかで2つに公倍数が存在するとき、(1以外の)(=互いに素でないとき) 2つの数の時より気を付けなければならない手順を踏む必要があるからです。
3つ以上の最小公倍数を求めるときにも連除算、はしご算を使います。
ただし、2つの数字で連除算を使うときはどちらも割れる数字で割っていき、どちらも割れなくなった時点で左端の数字から最後の数字をかけていくのですが、3つ以上の数になると、3つの内1つの数字が割り切れなくなっても、残りの2つの数字で一緒に割れる数字があれば最後まで割っていかなければなりません。
この点を注意して取り組みましょう。
3つ以上の最小公倍数、12と42と60の場合
12・42・60 ⇒共通で割れる数は2ですので2で割ります。
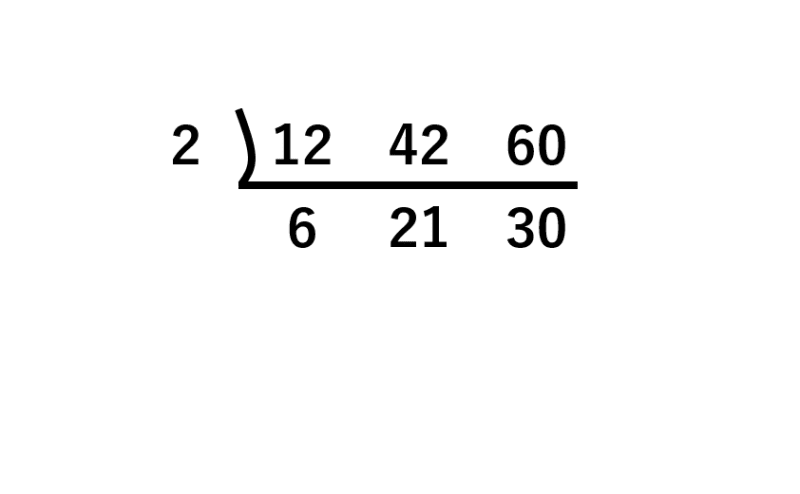
↓それぞれの数字を2で割った数
6・21・30 ⇒共通で割れる数は3ですので3で割ります。

↓それぞれの数字を3で割った数
2・7・10 ⇒共通で割れる数はありませんが、2と10は共通で2で割りきれますので7を無視して2で割ります。
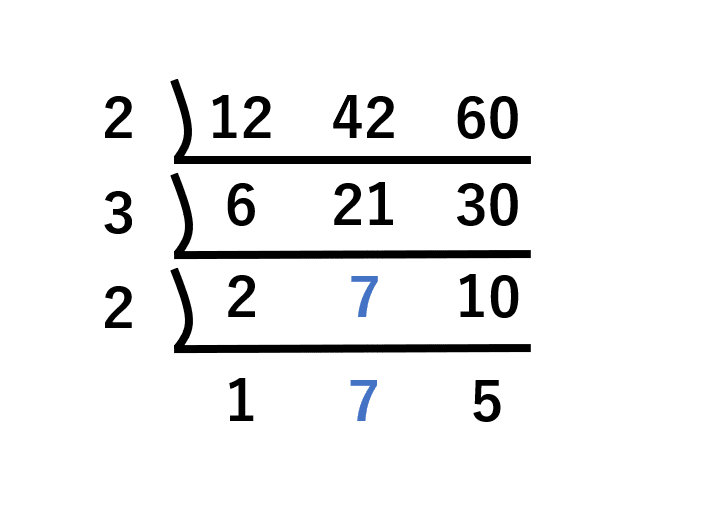
↓7を無視して2と10を2で割った数
1・7・5 ⇒3つとも共通で割りきれなくなった時点で終了です。
割った数が2・3・2、最後に残った1・7・5を全てかけ算をした数、2×3×2×1×7×5=420が最小公倍数であることが分かります。

小学生におすすめの通分の計算問題3選!

分数を倍分する問題
以下の分数の組の中で、最も大きな分数をそれぞれ選びなさい。
- (1/2 , 3/7)
- (1/2 , 4/7)
- (2/5 , 4/13)
- (1/2 , 3/7 , 11/23)
答え合わせ
- (1/2)=(7/14)、(3/7)=(7/14)なので、1/2の方が大きい。
- (1/2)=(7/14)、(3/7)=(8/14)なので、4/7の方が大きい。
- (2/5)=(26/65)、(4/13)=(20/65)なので、2/5の方が大きい。
- (1/2)=(161/322)、(3/7)=(138/322)、(11/23)=(154/322)なので、1/2が最も大きい。
4つ目の問題は少し難しいですね。
倍分(分子と分母に同じ数をかけること)をする時にどの数をかけたら良いのかわからないという時は、組になっている分母の値を全てかければ大丈夫です。
例えば、4番目の問題の場合は、1/2には残りの数字の分母である7と23の両方を分子・分母にかけます。その他の数でも同様に、3/7には2と23を、11/23には2と7を分子・分母にかけます。
こうすることで必ず全ての分数の分母が揃うので、困った時はこの方法を使うようにしましょう。
なお、4つ目の問題では、実は1/2以外の数は分母が分子の2倍よりも小さくなっています。
このことに気がつけば、わざわざ倍分するまでもなく1/2が最も大きな数であることが分かりますね。
最小公倍数を見つけた方が良い
分数の大きさを比較する際に、どの値で倍分するか迷った際は、互いの分母の値をそれぞれかければ良いとお伝えしました。
しかし、これは最終手段であり、基本的にはこれまでお伝えしてきたように最小公倍数を用いて倍分・通分をした方が圧倒的に良いです。
なぜなら、例えば3/1024と7/3072を比較する際に、わざわざ「1024×3072」のような計算を行うのは無駄だからです。
この場合、分母の最小公倍数が3072であることに気づけば、すぐに(9/3072 , 7/3072)の比較であることが分かるので、煩雑な計算を行う必要はなくなります。
異分母のたし算・引き算
以下の計算の結果をそれぞれ求めなさい。
- 1/3 + 2/5
- 10/6 + 2/3
- 4/5 - 18/24
- 1 - 9/10
答え合わせ
- 11/15
- 7/3
- 31/20
- 1/10
2番と3番は、まずは約分をしてから通分を行うのがポイントとなります。
また、4番は「1 = 10/10」であることを理解しているかがポイントと言えるでしょう。
通分が苦手な小学生へのおすすめ教材は?

通分を理解した後は練習問題でマスターしたいですよね。
そこで通分の練習におすすめの教材をご紹介します。
プリントや問題集で学習
小学校のうちは基本的には学校の教材だけで基礎をきちんとわかるようにしておけば中学の学習でも問題はありません。 ただ、ドリルなどの宿題をサボらずやることが大切です。
それでも多くの問題に触れたいと言う人は、ネット上にある単元別のプリントを使う、分数に特化した問題集を買うなどもおすすめですね。
通信教育もおすすめ
お子さんが算数を苦手にしている、もしくは実力を伸ばさせたいとお考えの方は、通信教育を受けさせることもオススメです。
最近の通信教育ではタブレット学習ができるものが増えています。 なかにはAIが苦手な問題を自動で出してくれるものもあります。
タブレット学習では、お子さんが楽しんで学習しやすくなるため、知らず知らずのうちに実力が向上することが期待できます。算数が苦手なお子さんも苦手を克服して勉強するモチベーションがわきやすいでしょう。
算数も含めて、おすすめの通信教育についてはこちらの記事で紹介しています。
通分・最小公倍数についてまとめ
通分・最小公倍数についてまとめ
- 通分をすれば分母が統一されて比較・計算できる
- 約分をすれば通分の比較・計算がしやすくなる
- 最小公倍数を求めるコツでさらに分数の計算が簡単になる
通分とは何かの解説と、通分をするために必要となる最小公倍数の仕方について解説してきました!
通分のやり方は分母をそろえるという点はマスターしたとしても、最小公倍数の求め方となると複雑で難しいと感じてしまうかもしれません。
通分が苦手だとお子様が感じられたら、ご家庭でも改めて通分のやり方と最小公倍数のやり方を確認したうえで、オススメ教材などでしっかりと復習していくことが大切です。
逆に通分をマスターすることができれば、素因数分解を学ぶときに応用していくことができますので、通分・最小公倍数のコツをつかんでいきましょう!







