【練習問題アリ】分数を理解しよう！苦手克服法から分子分母の意味・分数の種類まで解説

分数を言葉にして理解すると？

一つのものを何個かに切ったうちのいくつかを表すことができる数字のことを分数と言います。

分数は全体を1と考えるのですが、言葉だけを聞いても最初は理解することが大変難しいです。

そこでわかりにくい点は図で考えていきたいと思います。

分数はケーキで考えることが多いのでケーキを使ってみていきましょう。

丸いケーキを８つに切ったうちの3つ分、という量を表す時に3/8と表記します。

なお丸いケーキで考えることが多いですが、実際にはなんでも良くロールケーキのような棒状のものを使っても構いません。

3/8の場合、真ん中の線の上に表記している3を分子、線の下に表記している分母と呼びます。

式で考える

3/4というのは4つに切ったうちの3つ、ということです。

4つに切ったうちの一つは1/4と表せることから¾=3×1/4と表すことができます。

また、分数には割り算の意味もあり、1/4なら1÷4ということで1を4つに割った、という意味もあります。

3/4であれば3を4つに割るという意味で3÷4=3/4と表すことができます。

分数を式で表すと分かりやすいですね。

小学生の中でも、分数の計算に苦手意識を持つ子供は多いです。

分数が苦手になってしまう理由は？

分数が苦手になってしまう理由として、最も大きいのが「新しい概念である」という点でしょう。

抽象的な概念であるからこそ子供の理解が難しい分野でもあります。特に小学生低学年の段階から先取り学習で分数を学んでいる子供は、機械的にできはするものの本質的な理解はできていない場合も多いです。

そのため「なんでこうなるんだろう？」と考えこんでしまう子ほど、分数はよくわからないとなってしまうことも少なくありません。

小学5年生になれば、そういった抽象的な概念も理解できる能力が自然と身につきます。まずは機械でもいいので、分数の計算を間違えなくできるようにすることが重要です。

みんな苦手だからそのままでもOK？

このように、苦手意識を抱きやすい分数ですが、当然「他の子も苦手だから、うちの子も苦手で大丈夫」とはなりません。間違えずに計算ができる能力が身につくよう、しっかりとサポートをすることが重要です。

というのも、小学生での算数の苦手意識は、そのまま中学・高校での数学の苦手意識につながりかねないからです。早い段階で苦手を無くしておかないと、将来的な選択肢が狭まってしまいかねません。

「地頭が良くないと算数は得意にならない」と言われることも多いですが、そんなことはありません。できる限り年齢が低いうちから、算数に触れる機会を増やしてあげましょう。

分数の表記は3種類あります。

真分数、仮分数、帯分数の3つです。

それぞれの意味をよく理解して使い分けられるようにしておきましょう。

分子が分母より小さい真分数

真の分数、つまり1に満たない分数のことを真分数と言います。

真分数の読み方は（しんぶんすう）です。

真分数は1/2、2/3、3/4など分子の数が分母を上回らない分数を指します。

1998/1999のように分母がどれだけ大きくなっていても、分子が分母を上回らない分数は真分数です。

全体を１としてとらえて、その中に存在する数を表記するのが分数ですから、真の分数であると言っても良いかもしれませんね。

分子が分母と同じ・それより大きい仮分数

1個かそれ以上を分数で表す時に使うのが仮分数です。

仮分数の読み方は（かぶんすう）です。

5/5、つまり1や7/4など、分母の数と同じかそれ以上の数字です。

真分数の分数が本来の分数の形であるなら、仮分数は仮の分数であると考えましょう。

5/5は1ですから、分数表記しなくても良いですし、7/4は全体を1としてとらえているにもかかわらず全体の数を上回っているわけですから、本来の分数の形ではないと考えれば覚えやすいです。

整数と分数からなる帯分数

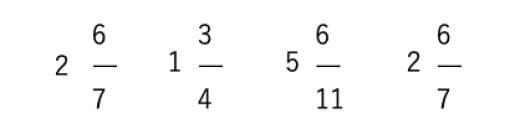
上記のように表記するのが帯分数です。

帯分数の読み方は（たいぶんすう）です。

また、例えば一番左の帯分数の読み方は２と7分の6です。

帯分数は仮分数と数が同じですが、全体を1としてとらえるものが2つあり、6/7が付随していることが見えやすい分数です。

仮分数よりも分数として用いられている部分が分かりやすいですが、計算をしづらい点もあるためか、中学からはほぼ用いられません。

帯分数を学んだ記憶はあっても、帯分数という言葉を忘れているお父さまお母さまはいらしゃるかもしれませんね。

仮分数・帯分数を変える方法

仮分数、帯分数はお互いに同じ数値であれば表記を変えられます。

仮分数から帯分数は、9/2なら、2/2が4つと1/2と考えられるので、４1/2　と表せます。

また、9/2をそのまま9÷2で計算し、答えが4…1となって答えの4が整数部分、あまりの1が分数の分子として帯分数を求められます。

逆に帯分数から仮分数は、整数部分を分数部分と同じ分母で表し、それを足し合わせれば良いです。

つまり、「7と3/5」を仮分数で表すなら、7＝5/5×7と考えて「35/5」とできるから、3/5と合わせて「38/5」と表せます。

分数には基本的なルールと問題の解き方が存在します。

ここをしっかり理解できれば分数の計算問題も簡単にできます。

約分

例えば3/6なら、上下両方とも共通して3で割れます。

その場合、3÷3=1、6÷3=2をして1/2として表せます。

図にすると、以下の通りです。

分数で表される数で、約分できるものは全てが同じ数です。

1/2、2/4、3/6、4/8と表される数値がどんなに大きくなっても、数の大きさは変わりません。

1/2も3/6も同じですし、10000/20000のような大きな数値であっても同じ大きさです。

通分

約分の性質で見た通り、分数については分母と分子に同じ数をかけ算しても、大きさは変わらない性質があります。

通分とは、この性質を使って、分数の分母を同じ数にそろえることを意味します。

つまり、4/7と2/3なら、分母を7と3の最小公倍数である21にすることを考えます。

4/7の場合、7を21にするには3をかけ算しますよね。

そうすると分母には3をかけ算したにもかかわらず、分子だけそのままにしておけませんので、分子である4にも3をかけ算し、4/7を12/21にします。

同じ様に2/3の分母も21にしますが、3を21にするには7をかけ算しますよね。

分子にも同じ7をかけなければなりませんので2×7=14となり、2/3は14/21と表せます。

すると、12/21と、14/21となって分母がそろいます。

分母がそろうことで分子を見たら大きさの比較ができ、さらに足し算と引き算を行うことが可能になるので、通分は分数には欠かせない存在だと言えます。

割り算として分数を考える

分数は1に満たない数を表しますので、小数に表すことが可能です。

例えば3/4なら、3÷4の計算式に表せますので、そのまま割り算の計算をすれば3÷4=0.75と表せます。

なお、1/3の場合は1÷3=0.3333333…と割り切れなくなり、小数で表すことができません。

割り算の計算をしたとき、割り切れない数字も一つの数値として表せるのです。

通分のたし算・引き算の問題

以下の計算の結果を求めよ。

1. 1/2 + 1/3
2. 1/4 + 1/2 + 1/6
3. 3/8 + 5/6
4. 1 + 1/3
5. 4/5 - 7/13
6. 3 - 2/5

解答解説

1. 5/6
2. 11/12
3. 29/24
4. 4/3
5. 17/65
6. 13/15

分母の違う分数のたし算・ひき算では、まずは通分からスタートします。

通分の際は、分母を最小公倍数に揃えましょう。例えば、2番の問題ではそれぞれの分母である「4」「2」「6」の最小公倍数の「12」に分母を揃えることで、スムーズに計算を進めることができます。

分数を小数に直す問題

以下、それぞれの数字において、分数は小数に、小数は分数に直しなさい。ただし、分数に直す際はこれ以上約分できないものを示しなさい。※

1. 1/5
2. 3/8
3. 0.75
4. 0.125

※正確には、分子と分母が「互いに素」の分数で表せ、という指示になる

解答解説

1. 0.2
2. 0.375
3. 3/4
4. 1/8

1番と2番については、分子を分母で割ればすぐに答えを求めることができます。

3番と4番では、小数を分数として捉え直すことから始めます。つまり、4番の場合は「0.75 = 0.75/1」と考えます。あとは、分子と分母に4をかけることで、分子が整数になることに気づけば良いです。

分数の苦手を克服するにはどのようにすれば良いのでしょうか。

以降では、分数の苦手の段階的な克服方法をご紹介します。

分数の概念を丁寧に理解する

分数の概念を理解するには、「割って考えられる物」のイメージをするとわかりやすいです。ここでは、例としてピザを取り上げてみます。

ピザは切っていない1枚の時は「1」です。ですがこれを4人で食べるために、4等分に切り分けた時、それぞれのピースは1/4と数えられますね。

また、このピザを１/4が2枚あると2/4になりますが、これはピザを二等分した1/2と大きさが同じですね。このように、異なる数字であっても同じ数を表すことがあります。

このように、視覚的イメージを伴って勉強するようにすると、抽象的概念が理解しやすくなります。

約分について理解する

上記のように、1/2と2/4や3/6などは異なる数字ながら同じ意味を持ちます。このような数字は、約分を行うことが必要です。

約分をすることで計算が楽になりますし、約分をした形を回答に書かないと減点されてしまうことも多いです。そのため、約分の癖をつけるトレーニングをすることが必要となります。

分数が出てきたら、「上と下、どっちも割れる数字は無いかな」と約分を探すことを習慣づけるようにしましょう。

通分の概念を理解する

分数の足し算・引き算をするためには、通分をマスターする必要があります。そのためには、異なる数字の最小公倍数を自然にできるようになることが必須です。

最小公倍数は「素因数分解→共通しないものを、共通するものにかける」というプロセスで機械的にに求めることができるので、実際にやってみましょう。

例えば、15と10の場合、素因数分解をするとそれぞれ「15＝3×5」、「10＝2×5」ですので、共通しないものは2,3、共通するのは5ですね。

そのため、15と10の最小公倍数は2×3×5=30となります。「10と15の最小公倍数は30でしょ」と感覚的にわかる方も多いと思いますが、小学生のうちはこのように練習をさせてあげましょう。

ただし、当然分子にも掛け算を行うことを忘れないようにしましょう。

帯分数と仮分数の計算を完璧にする

帯分数とは、分子＞分母の時に整数だけ括り出して、整数と分数をセットの形で表した分数のことです。一方で、仮分数は分子がどれほど大きくとも帯分数にせず、32/3のように表す分数のこととなります。

数学になると帯分数を利用することはほとんど無くなりますが、小学生の算数では帯分数に直すことを習慣づけることが必要になります。

約分と同様に、仮分数→帯分数に直すことも常に意識して行うようにしましょう。

分数を理解できているかを確認するには練習問題を解いてもらうのが一番です。

ここではおすすめの教材をご紹介します。

ドリルを使って学習する

小学校のうちは基本的には学校の教材だけで基礎をきちんとわかるようにしておけば中学の学習でも問題はありません。

特に小学4年生までに触れる分数は、分数とは何かを知るだけで大丈夫です。

しかし、約分や通分が本格的に導入される小学校5年生の勉強ではドリルなどの宿題をサボらずやることが大切です。

小学生の算数で「わからない」は基本的に慣れていないものを放置してしまっているだけなので、まずは学校の教材・宿題をしっかりとこなすことが、基礎形成に良いです。

中学受験の算数対策は受験塾もおすすめ

大手の受験塾であれば大抵どこも同じですが、オリジナルテキストが使用されております。

また、難関私立の中高一貫校に向けた対策ができ、頻出問題を分析して作成してあるテキストは受験対策に対応することが可能です。

オリジナルテキストは答えにも丁寧に解説が掲載されているので、見直しをするだけでも実力がつきます。

これをしっかりやるのが受験にとっては最も近道です。

以下の記事では、中学受験に向けた塾の選び方やおすすめの塾について、紹介しています。受験塾についてより詳しく知りたい方は、こちらの記事もぜひご覧ください。

中学受験塾の選び方のポイントは？合格実績や比較時の注意点・おすすめの塾まで紹介！

通信教育もおすすめ

最近の通信教育ではタブレット学習ができるものが増えています。

タブレット学習では、お子さんが楽しんで学習しやすくなるため、知らず知らずのうちに実力が向上することが期待できます。算数が苦手なお子さんも苦手を克服して勉強するモチベーションがわきやすいでしょう。

算数も含めて、おすすめの通信教育についてはこちらの記事で紹介しています。

【2024最新】小学生向け通信教育ランキング｜おすすめ17社を徹底比較！

一言で分数と言っても、小学生に分かりやすく説明するには事細かく丁寧にしなければいけません。

分数を小学生の間にマスターしておかなければ、中学生になったときには当たり前のように計算問題から文章題、図形問題で登場しますので大苦戦してしまいます。

ご家庭でも分数の計算問題にたくさんチャレンジして、苦手対策を行っていきましょう！