【速報】2021共通テスト数学IAは難化?Twitterの口コミや問題傾向を徹底分析!
更新
2021年 共通テスト「数学IA」の試験データ
| 項目 | データ |
|---|---|
| 実施年月日 | 2021年1月17日 |
| 実施日時 | 11:20~12:30 |
| 試験時間 | 70分 |
| 大問数 | 変化なし |
| 難易度 | 例年なみ〜やや難化 |
大問数・設問数・マーク数は上記のように変化しました。
難易度は、センター試験に比べると全体として難化しており、出題形式もセンター試験や試行調査から大きく変化しました。
平均点については、2021年1月20日(水)に大学入試センターのホームページにて公開される予定です。
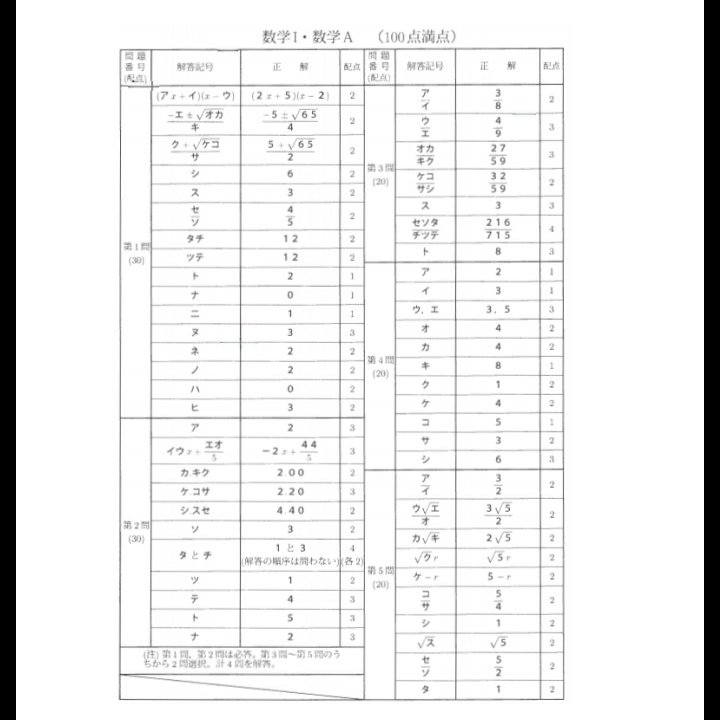
数学ⅠAの配点と模範解答
2021年 共通テスト「数学IA」試験の感想・口コミ
今回の試験についてSNS上の口コミを見てみましょう。
【総評】
上の口コミのように大手予備校教師からは難化という感想が寄せられました。
【第1問】
上の口コミのように基礎的な出題が多く、計算ミスに注意して満点を狙うべき大問でした。
【第2問】
第2問[1]では上の口コミのように陸上競技における文章題が出題され、専門用語に戸惑いスラスラ読み進められなかった受験生も多かったようです。
第2問[2]では上の口コミにみられるようにデータの分析の配点が高くなっている事にショックを受けた受験生も多くみられました。
【第3問】
第3問は誘導が丁寧であったものの3桁分の3桁が答えになるような問題があり計算量が多く完答は難しかったようです。
【第4問】
第4問は整数は簡単という口コミと難しいという口コミがちょうど同数程度みられました。文章題をいつもの整数問題に落とし込める事に気づければ簡単、気付けなければ難しかったのではないでしょうか。
【第5問】
第5問は最も難易度が高いという口コミが散見されました。
上の方のように選択問題であったため他の大問を選んでおけば良かったと感じている方もいらっしゃるようです。
設問ごとの難易度と重要問題を分析
以下でトータルの総評とそれぞれの設問ごとの評価をしていきます。
【総評】
文章をしっかり読まないと解けない問題が増えたものの、問題自体の難易度は上がっていないと言えるでしょう。また、10分試験時間が増えたにもかかわらず、特別捻りのある問題が出題されている訳ではないので、むしろ時間内に解き終えること自体は易しくなったと言えます。
しかし細かな引っ掛けややや解きにくい問題も存在するので、以下で大問ごとに詳しく解説していきます。
第1問
第1問[1]は因数分解などの作業を必要とした「数と式」からの非常に基礎的な出題が見られました。
少々計算が煩雑ですが、解の公式に当てはめてサクサク解いていきたいところです。旧帝大や医学部、早慶を目指す方は5分以内、日東駒専やMARCHを目指す方も10分以内で完答を目指しましょう。
第1問[2]は三角比に関する簡単な公式を利用する「図形と計量」からの出題でした。
(1)は公式をただ利用すれば良いものの、(2)(3)は三平方の定理を学んだときに、直角以外だとどうなるかということを確かめた方には馴染みのある出題だったのではないでしょうか。
馴染みのない方は面食らったかと思いますが、Aの角度を30°、60°、120°などよく見る角度で仮定して計算してみるとイメージがわくのではないでしょうか。
第2問
第2問[1]は陸上競技において具体的な最速タイムを求める文章題であり、「二次関数」からの出題でした。
問われていることは簡単ですが「ストライド」、「ピッチ」という新しい言葉が定義付けされているので文章をしっかり読むことがカギです。また(1)を間違えてしまうと(2)の途中から連動してミスをしてしまうので何度も見直してください。
(2)ではストライドが大きくなると、ピッチが小さくなることからxの係数が負であることに素早く気づくことが大事と言えるでしょう。
第2問[2]は3つの産業の就業者のデータを読み取る「データの分析」からの出題でした。例年より配点が高くなっています。
箱ひげ図やヒストグラムの読み方、四分位数の定義、相関係数についての細かな知識があれば確実に正解できる問題だったでしょう。
センター試験時代と問われていることが変わらず、どれも基本的であったことから確実に完答したい大問と言えます。
第3問
くじ引きにおける「確率・場合の数」からの出題でした。
(1)(3)は反復試行、条件付き確率についての基本的な問いです。(2)は「同じ数字で掛けたり割ったりしても比の値は変わらない」という当然のことを考えれば良いのですが、少し見慣れないため戸惑った方もいるのではないでしょうか。
(4)は太郎の「条件付き確率の値は計算しなくてもその大きさを比較できるという」という発言からうまく誘導に乗っていきたいところです。
第4問
石を時計回りや反時計回りに移動させるゲームを「整数」に関する問題に落とし込んだ出題でした。ヒントに記載があるものの、文章題を整数に落とし込んでいるところが理解しにくいと思った受験生も多いのではないでしょうか。
(1)で求めた答えが不定方程式5x-3y=1の解になっているというヒントからいつもの整数問題と変わらないことに気付けたのではないでしょうか。
ヒントに気づくと(2)もこれまでの整数問題より難易度が低く絶対に完答を狙える大問であったと言えるでしょう。ヒントに気付けるかが、勝負の分かれ目です。
第5問
典型的な「図形の性質」からの出題でした。
出題されている三角形の辺の長さが「3:4:5」であるため、早い段階で直角三角形であることに気づけたかが勝負の分かれ目と言えるでしょう。
前半は角の二等分線の公式、三平方の定理など基本的な公式を利用し、後半は方べきの定理と内接円の性質からうまく誘導に乗ることができればスムーズに解けたでしょう。
なお、最後の同一円周上にある問題は、時間的な制限を考えると解き切るのが難しく、捨て問題とした受験生も多かったかもしれません。
総評と今後の対策
ここからは追試験を受ける方や来年度以降の試験を受ける方についてのアドバイスをしていきます。
計算力をつけよう
文章の量が増えたことで後半の設問に時間費やさなくてはならない時間が増えたことから、第1問をいかに早く正確に解くかということの重要性が増しました。
そのためにはしっかりと計算力をつけることが大事です。計算の訓練をする際にはストップウォッチで時間を測りながら取り組むのも良いでしょう。
また第3問(3)のように3桁分の3桁の確率を求めさせるような出題が今後も続くかもしれません。
したがってこのような複雑な値が出た時にすぐ検算や見直しできるように自分なりの方法を確立しておくと良いでしょう。
データの分析は対策必須
今回の共通テストでは第2問[2]で出題された「データの分析」の配点が増加しました。
「データと分析」は学校では大きく扱わないところが多いものの、抑えておかなければならない公式や用語の定義などが多いため後回しにせずに余裕を持ってしっかり取り組むことが大事と言えるでしょう。
一度頭に入れておくと復習もしやすいため定期的に確認することが大事です。
ヒストグラムや箱ひげ図などの図、四分位数・分散・標準偏差・共分散・相関係数などの用語について人に説明できるまでしっかり理解しましょう。
日常の出来事と関連付けよう
第2問[1]や第4問のように日常的な出来事を数学に落とし込んだ出題がみられました。
今回の出題だと特に第2問[1]では馴染みのない専門用語が出てきたのでそれだけで面食らってしまった受験生もいるでしょう。
しかし専門用語は必ず定義づけされていたり、補足説明があります。
したがって、そこで焦ることなく誘導に乗って立式することが大事ですので練習を重ねて慣れていきましょう。共通テスト対策専門の問題を繰り返し解くのも重要です。
さらに、普段ならった公式が日常生活ではどのように応用されているのかイメージしてみるのも良いでしょう。
共通テストⅡBの速報も参照
共通テスト数学は、ⅠAでは例年並みの難易度だったものの、ⅡBの難易度はかなり易化したようです。
IIBの出題傾向や問題形式はⅠAを勉強する時の参考にもなるので、是非この機会にチェックしておきましょう。
来年度以降に共通テストをうける受験生の方へ
来年度以降に共通テストを受ける場合、一番気になるのが「傾向が変わるのか」ということでしょう。
実はセンター試験が開始した時も、開始後の数年間は傾向がぶれてしまっており、対策がしにくい状況でした。
そんな中で受験生に必要な行動が「情報収集を徹底する」と「演習を重ねる」の2点です。
共通テストでは、この先どのような傾向の問題が出てもおかしくないわけですから、大学入試センターの発信する情報はもちろん、予備校各社の出す分析や学校の先生の講評などをしっかり聞いて自分なりに分析を重ねていくことが大切です。
また、本番どのような問題が出てきても解けるように、普段から様々なパターンの問題に取り組んでおくこともおすすめします。
予備校の出版する予想問題集や通信教育で受講することができる「共通テスト対策講座」などを利用することで、多様な問題に触れ、過去問や試行調査と全く異なる問題傾向での出題があっても対処できるような訓練を積むことができるはずです。
共通テスト数学対策は通信教育・予備校でばっちり
共通テストの数学対策を行うなら、通信教育・予備校で効果的に対策を進めていきましょう。
試験の傾向を各社徹底分析したうえで、得点力を効果的にアップできるように教材・指導を組み込んでおり、独学と比較しても必要な能力を効率よく身に付けることができます。
また、数学の得点力アップに欠かせない問題演習の機会もう豊富に設けられているため、アウトプットもばっちりです。
以下の記事では、通信教育・予備校各社の特徴について詳しく解説しているので、こちらも併せてご覧ください。






