算数の難問の解き方は?得意な子供の思考や解ける必要性・中学入試での対策法まで解説
「算数の難問の解き方は?」
「得意な子供の思考や解ける必要性はあるのか?」
このように疑問に感じる方がいるでしょう。
算数の難問を解くには、どのような方法があるのか気になるはずです。
小学生の中には実際に難問を解ける子供もいます。
そのような子供の思考・解く必要性・中学入試での対策法まで詳しく説明していきましょう。
最後まで読んだ方は、子供と力を合わせながら勉強に取り組んでいけるはずです。
算数の難問の解き方についてざっくり説明すると
- そもそも難問を解く必要はあまりない
- すぐに難問を解ける子供もいる
- 1つの問題を解く際に複数の視点から見るようにしよう
算数の難問への向き合い方

小学生の子供が「難問」を解くことは必要なのか、どのように解いているのかを疑問に感じている親は多くいます。このように感じている親の疑問を解決していきましょう。
難問は解けた方がいいの?
基本的には子供は、相当な難問を解くことができる必要はありません。
小学生で難問を解く機会は、中学受験の時にある可能性があります。日常生活で難問に関して、問われることはほとんどないはずです。
小学校のテストで難問を出題されることや大学の受験まででも問われる機会は、少ないでしょう。余程のことがない限り、難問を解く機会はなかなかありません。
難問に解く機会は少ないですが、遭遇する機会がゼロではないでしょう。難問を解くためには「思考力」・「根性」・「計算スピード」が必要になります。
そのため、難問を解ける能力があった場合は本人にとって大きなプラスです。そこまでの能力があるのは、凄いことです。難問を解くための能力は身に付けようとしても、簡単にできることではないのです。
中学入試で出題されることも
小学生で難問を解ける必要はありません。しかし、中学受験を検討している場合は例外も充分にあり得ます。
受験する学校の過去問で出題された難問については、しっかりと試験対策をし、繰り返し挑戦するべきです。
試験対策を行っていなければ、本番で焦ってしまいます。他の問題を解く際にも良くない影響が出る可能性もあります。
試験対策として、過去に出題された難問を解くことは大事です。ただ、簡単に解けるわけではないので、相当な時間がかかるはずです。
もし、時間がかかっても難問を解くことができれば、本試験では自信を持って挑めるでしょう。難問が解けたことは子供にとって、大きな影響を与えます。
また、難問を解ける子供の「特徴」・「能力」・「経験」などを分析することも大切です。問題を解くための何かしらのコツやきっかけが掴めるでしょう。
問題を解くだけではなく、実際に難問を解いた子供がどのようなことをしているのか、分析もしてみましょう。知り合いの場合は、詳しく話を聞いてみても良いです。
すぐに解ける子供も存在する
算数は勉強を重ねていくと一定のレベルで、向きと不向きに分かれてしまいます。元々の素質も関係しており、あまり勉強をしていなくても難問が直感で解ける「天才」と呼ばれる子供も存在します。
直感で問題が解ける「天才」と呼ばれる子供は、並外れた才能を持っている場合が多いです。ただ、このような子供になるのは難しいでしょう。
「神童」と呼ばれる子供はごく少数です。受験では「天才」・「神童」と呼ばれる子供ではなくても充分に問題を解くことができるという設定の場合がほとんどなのです。
ですから、受験をする時は、しっかりとした試験対策を行えば難問でもすぐに解けるようになるという可能性は大いにあるのです。
難問を解ける子供は思考が違う?

難問を直感で解ける「天才」・「神童」と呼ばれる子供がいます。その子供は一般の思考とどう違うのか、気になってくるでしょう。一体、どのような思考になっているのかを見ていきましょう。
いくつもの考え方ができる
難問を解ける子供は多くの問題を解いていく時に、1つの問題に対して様々な視点から解くことができます。基本的には1つの問題を解く時は、決まった方法で答えを導こうとする場合が多いはずです。
これは、レベルの高い問題を数多く解くことで複数の解き方があることを事前に学んでいるのです。
これによって子供は自分の中で「解法の引き出し」をどんどん増やし、試験中にも問題を解く方法が1つではなく、複数あることに気付けるようになります。
様々な視点から解く方法が定着してくると、類似した問題が新たに出題された時はどのような解き方をしようと考えるのです。
難問を解く時にも基礎的な方法を組み合わせて、問題を解いていきます。複数の基礎的な方法を自らの頭の中から上手く引き出せるのかが重要です。
1つの方法に固執せずに、様々な視点から別の解き方を導くようにできると最終的に難問を解けるでしょう。
思考スピードが速い
様々な視点から問題を解いていく方法を身に付けた後は、順番に試していくことです。
1つ目の方法に試みた時に失敗した場合は、次の方法を挑戦するという流れになります。この時に大事なことは、ある方法では解けないということを見極める力やこの方法なら解ける可能性があるといった先を見通すことです。
問題を解く時に複数ある方法から、1つの選択肢を選ぶことは途中までの見通しをつけるために早く判断しなければなりません。多くの問題数に挑んで解く方法や流れを把握して、頭の中にすぐ浮かぶことができるようにしましょう。
問題が解けても別解を考える
難題を解けた時に時間がかかったり、計算量が多い方法で解いたはずです。その時は達成感がとてもあったでしょう。ただ、達成感を味わえてもそこで満足してはいけません。
問題を解けた方法であっても、必ずしも最短で解けたとは言えないでしょう。かなり遠回りをして、複雑な計算をしている可能もあります。このような場合もあり得ますので、1つの解き方に固執しないようにしましょう。
問題を解く時には別の解く方法があると考えるようにすると、新たな発見があるはずです。様々な視点から1つの問題を解いて、1つでも多くの方法を見つけるようにしましょう。
友達と解説し合うのもおすすめ
難しい問題に出会った子供は、レベルの近い友達に一度相談してみましょう。友達と難しい問題について、解説をし合ったりすると良いです。また、相手の解釈を聞くことで、新しい考えた方や気付かなかった見方を知ることができます。
1人で問題を解いていると同じ視点になりがちになるため、友達から新たな視点を教えてもらうことも大事です。問題を改めて解説することになり、自分の理解にもつながるでしょう。
自分以外の人物と話し合うことは新たな発見や自らの理解度を確かめる2つの役割があり、積極的に行うと良いです。もし、友達が相談してきた時は親身になって話を聞くようにしましょう。
大体の難問は数をこなせば慣れる
受験で出題される問題の中で難しい問題がある場合は、解く方法が存在しているでしょう。これは難しい問題にも、解き方のパターンがあると言うことです。難しい問題でも対策を取れば、解くことができないわけではありません。
最初に基礎的な部分を学んでから、応用の解き方を定着できるようにしましょう。問題を解くには、まず基礎から入り応用へと繋げていくことが重要になってきます。
有名な難問は、解き方の手掛かりが見つけにくくなっています。正解に近付くためにはパズルや知恵の輪を解くような形になっており、何かヒントを探す必要があります。
対策方法としては、あまり気合いを入れ過ぎずにゲーム感覚で試してみると良いです。
パズルや知恵の輪に行う時には「ひらめき」も大事になってきます。これを難しい問題を解く時に取り入れてみるとコツを掴める可能性があります。難しい問題にもどんどんチャレンジしてみましょう。
小学生向け算数の難問・良問3選!

橋を最速で渡れる方法は?
問題
夜、4人の小学生A君、B君、C君、D君がグラグラする吊橋を渡って宿に戻ります。この夜、彼らは懐中電灯を1つしか持っていませんでした。吊橋は危険なので、懐中電灯なしでは渡ることができず、さらに橋には常に2人を支えるだけの強度しかありません。
彼らはみな歩く速さが違い、それぞれ橋を渡り切るまでに最短で以下の時間がかかります。
- A君・・・1分
- B君・・・2分
- C君・・・5分
- D君・・・10分
この時、彼らは最速で、何分で全員が橋を渡り切ることができるでしょうか?
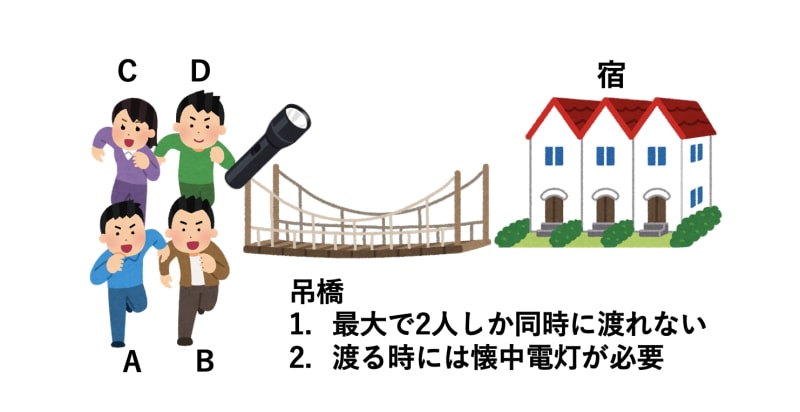
思考力・ひらめき力を試される問題です。粘り強くいろいろなパターンを考えてみましょう。
解答・解説
(解説)
- A君とB君が同時に渡る(累計2分)
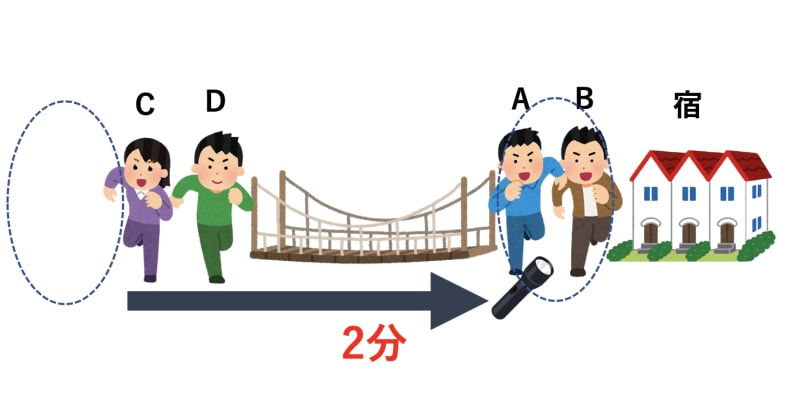
- A君が懐中電灯を持って帰ってくる(累計3分)
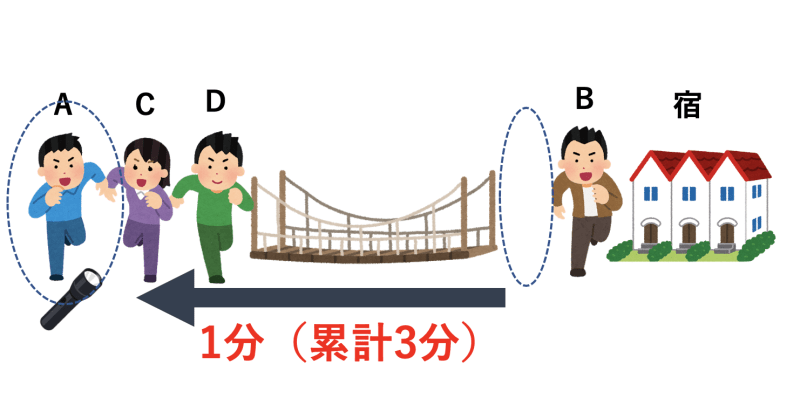
- C君とD君が同時に渡る(累計13分)
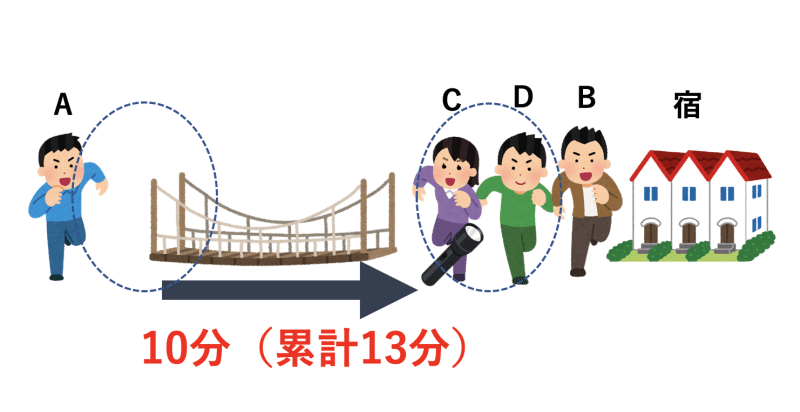
- B君が懐中電灯を持って帰ってくる(累計15分)
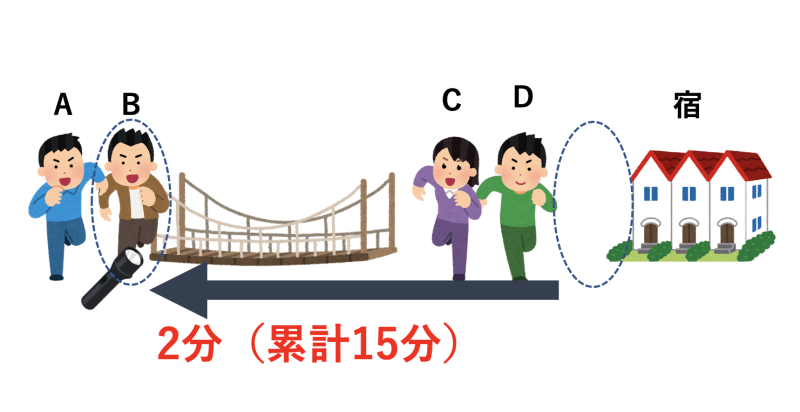
- A君とB君が同時に渡る(累計17分)
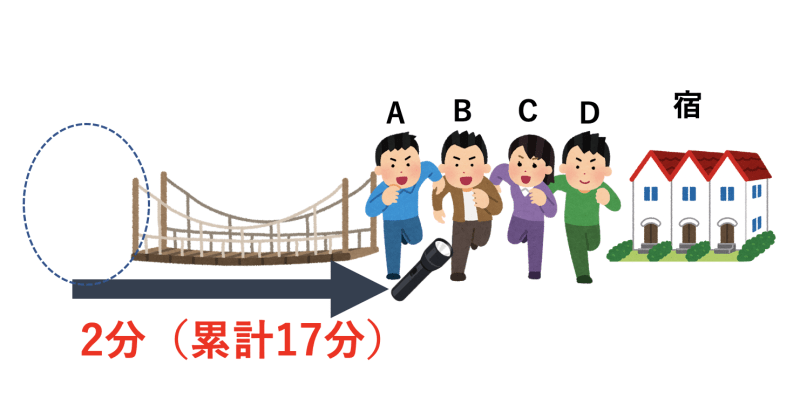
(解答)17分
モンティ・ホール問題
モンティ・ホール問題は、状況を正しく整理する力を試される問題です。
問題
いま、挑戦者のあなたの前には、3つの扉があります。
そのうち1つは「アタリ」で、2つは「ハズレ」の扉です。
あなたは3つの扉の中から1つだけ扉を選びます。もし「アタリ」の扉を選ぶと賞金100万円をもらうことができます。
あなたが1つの扉を選んだあと、司会者のモンティは「アタリ」の扉がどれかを知っているので、あなたが選ばなかった2つの扉のうち「ハズレ」の扉をひとつ選んで開けてくれます。
このあと、あなたは最初に選んだ扉をそのままファイナルアンサーとすることもできるし、もう一度だけ回答を変更することもできます。
この時あなたは回答する扉を変えるべきでしょうか?変えないべきでしょうか?

解答・解説
(解説)
これは「モンティ・ホール問題」と呼ばれる問題です。解答・解説を読んでもなかなか納得できないという有名な問題です。
モンティ・ホール問題の、よくある誤答として
『司会者がハズレの扉を開けて、扉が2つに減った。今から回答を変えた時に「アタリ」の扉を選ぶ確率も「ハズレ」の扉を選ぶ確率も50%だから、回答は変えなくて良い。』
という回答があります。
直感的に考えるとこのような誤答をしてしまうのですが、じっくり考えると誤答であることがわかります。
正しくは次のように考えます。
- 最初に「アタリ」の扉を選ぶ確率は1/3、つまり、選ばなかった2つの扉に「アタリ」の扉が含まれている確率は2/3です。
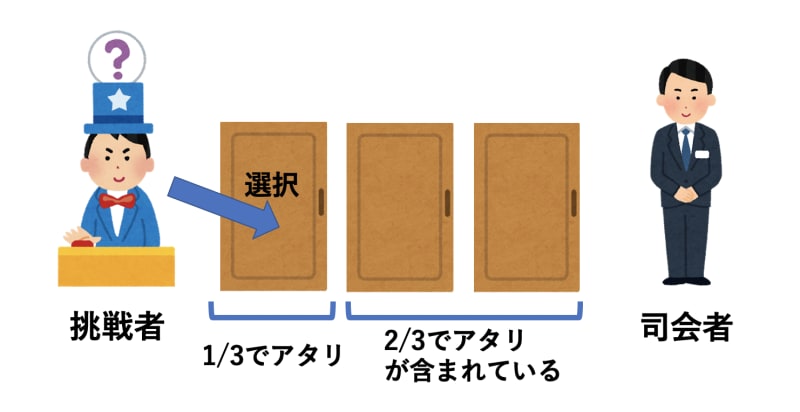
- この時、選ばなかった2つの扉のうち、必ずどちらかはハズレです。そして、司会者モンティは選ばなかった2つの扉のうち「ハズレ」を確実に開けてくれます。
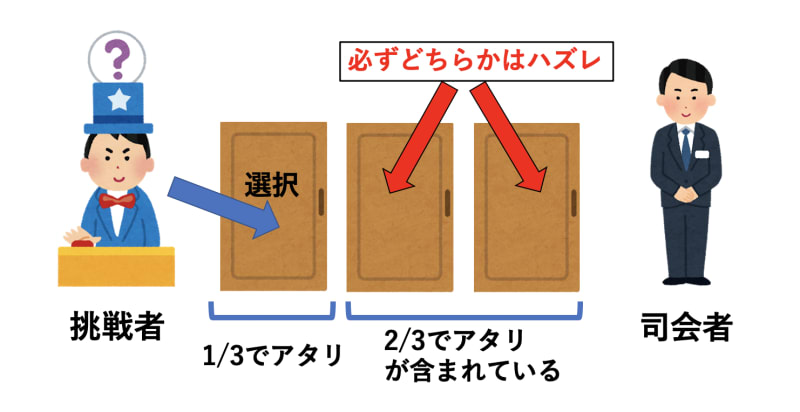
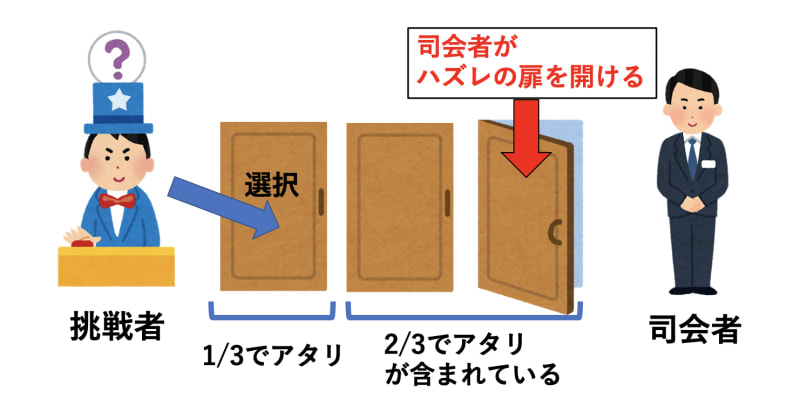
- 残された2つの扉のうち、選ばなかった方の扉が「アタリ」である確率はそのまま2/3です。
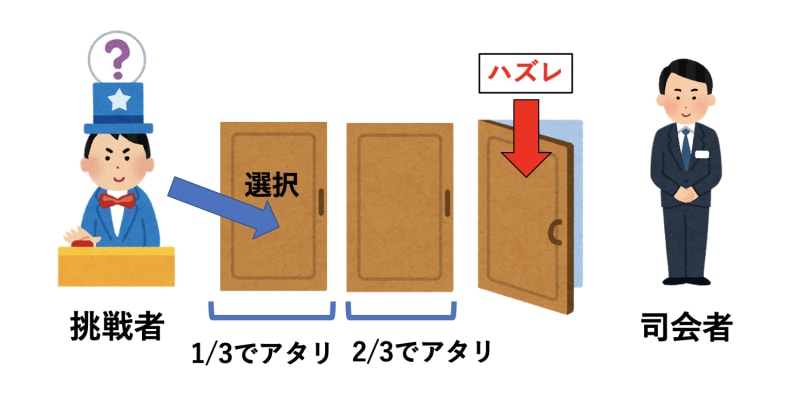
- 選択を変えた方がアタリの扉を選ぶ確率が1/3から2/3に上がります。
この解答を読んで「なるほど。言われてみればそうだけど…」となりませんでしたか?
モンティ・ホール問題は直感だと誤答してしまいますし、論理的に考えた解答もどこか腑に落ちない、非常に厄介な問題ですね。
(解答)変えるべき。変えた場合、アタリの扉を選ぶ確率は2/3であり、変えない場合、アタリの扉を選ぶ確率は1/3である。
等しい長さをもつ三角形の問題
小学生向けの図形問題の中では難易度の高い問題となっています。多くの場合、図形問題では「補助線」を引けば解決できることが多いですが、この問題では少し斬新な発想が求められます。
問題

三角形ABCにおいて、BC上に点Dをとる。
∠ABC = 40°、 ∠BAD = 30 °、AB = CD である。
この時、∠ACB の大きさを求めなさい。
解答・解説
(解説)
- ABとCDの長さが等しいことに注目して、三角形ABDを切り取ります。
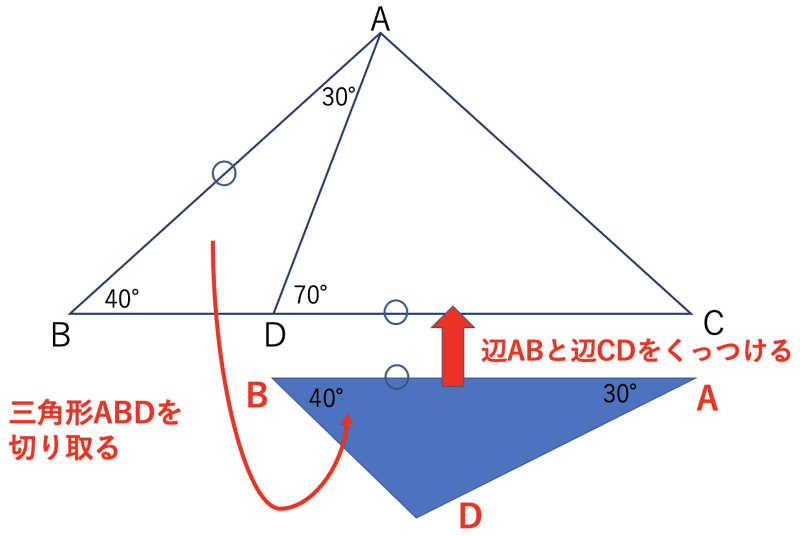
- ABとCDをくっつけて、台形DD"CAを作ります。
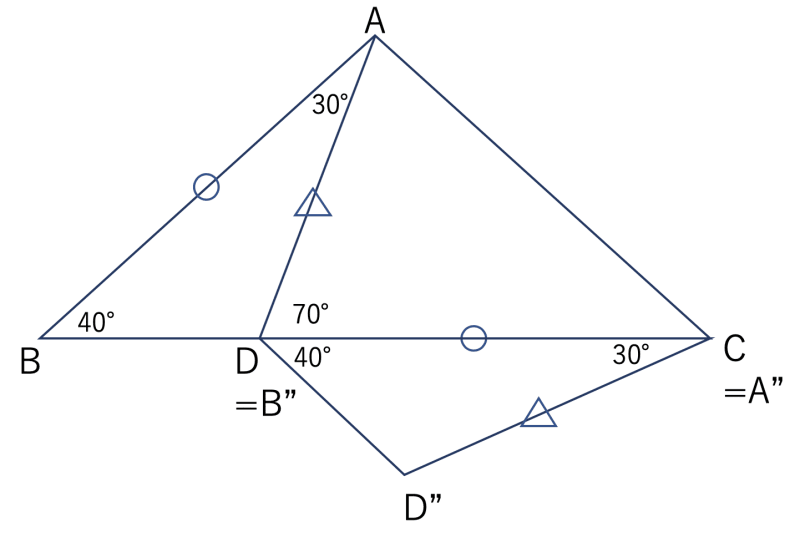
- 台形DD"CAは、DA=D"C、及び、∠ADD" = ∠CD"D =110° なので、等脚台形です。
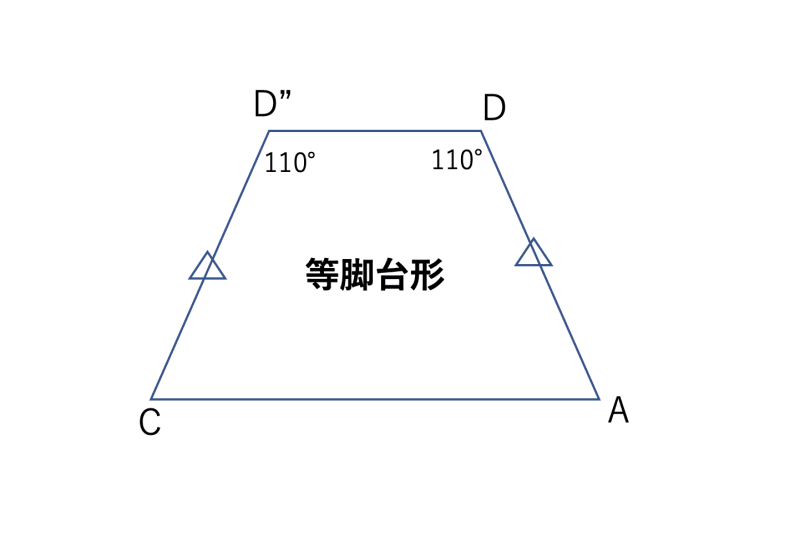
- 等脚台形DD"CAでは、内角の和が360°であることと∠DAC = ∠D"CAであることから、∠DAC = ∠D"CA = 70°になります。
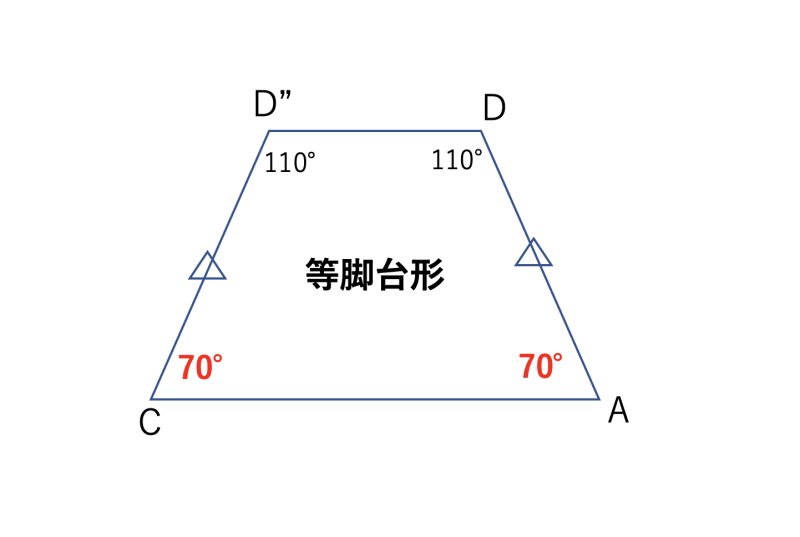
- よって、∠ACB = 70° - 30° = 40° となります。
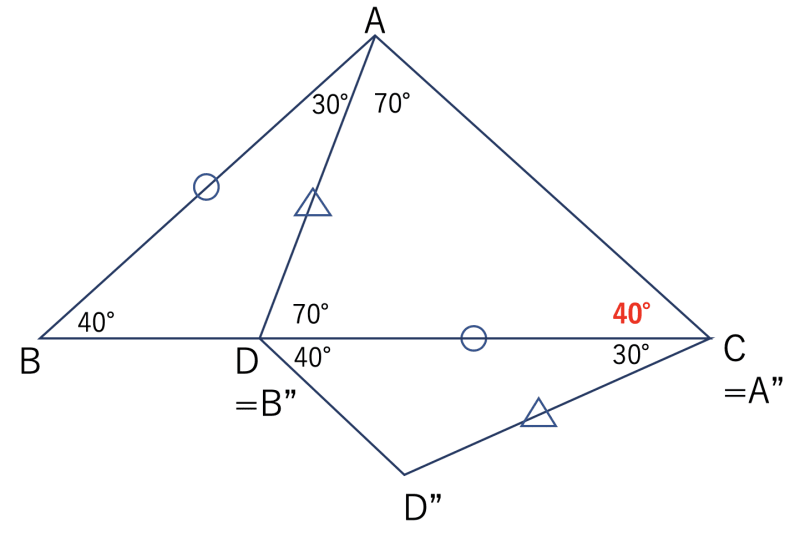
(解答)40°
難問はどこで手に入れる?

難問を解くためには自分以外の人物と話し合ったり、ゲーム感覚で解くなど様々な方法を試してみましょう。
個人だけでは見つけることができなかったコツが手に入る可能性もあります。自分のやり方に偏ってしまわないように気を付けましょう。
次に、難問を手に入れる方法を伝えていきます。難しい問題を解こうとしても問題自体がなければ、困ります。どこで手に入れることができるのか見ていきましょう。
WEBサイトでも豊富
まずは算数や数学の難問については、インターネットで数多くの問題が載っているでしょう。自分が思う以上に多くの難問を見つけることができるはずです。
しかし、難問のレベルが高校生が解くレベルで小学生には解くことができない問題が多くなっています。小学生の中には解ける子供もいるでしょうが、ほとんどいないでしょう。
最初から難し過ぎる問題を解くと、子供が自信を無くしてしまう可能性が十分あります。せっかくの解けそうな雰囲気を壊さないように気を付けて、良問に挑んでいきましょう。
インターネットにある難問は、直接学校の成績に影響を及ぼしません。そのため、インターネットで見つけた難問を解く場合は遊びの感覚で行うと良いでしょう。遊びの感覚で解くことで、新たな発見ができるはずです。
レベルの高い問題に挑戦することは良いことです。しかし、あまりに違うレベルの問題を解くことは避けた方が良い場合もあります。まずは、子供のレベルに合った問題から始めていきましょう。
志望校の入試問題を利用する
中学受験でレベルの高い問題が過去に出されたことがある場合は、その過去問を解いてみると良いです。実際に出題された問題を解くことで、本番さながらの経験ができます。
また、難問が出題された学校の問題の傾向や対策する方法を知ることが可能です。
多くの難問を解くことも大事ですが、子供が目指している学校の問題に触れるようにしましょう。受験の際に、似たような問題が出題される可能性も十分あります。
難問を解く方法の1つとしては、多くの難問に挑戦していくことです。また、受験用の難問に関しては、一定の解き方が存在します。問題を何度も解いていけば、解き方の法則が見つかるでしょう。
受験のための難問対策なら塾もおすすめ
中学受験を考えている場合は、塾に通って勉強をすることをおすすめします。受験にはある程度決まった傾向が存在します。それは決まった問題の解き方があり、個人で試験対策するには限界があるのです。
例えば、私立中学の受験を希望している場合は、周囲のレベルを知るべきでしょう。学校ごとに受験対策の講習があるため、可能であれば塾に通った方が良いです。
塾に通うことで試験の傾向や試験対策をしっかりと行えます。また、周囲には同じ学校を目指す子供もいるため、良い刺激を受けるでしょう。周囲と切磋琢磨しながら、受験に挑むことができます。
塾や通信教育の発展学習で
通信教育ではレベルごとの学習方法があり、発展学習の教材も存在します。レベルが高すぎない難しい問題が解きたいのであれば、通信教育に入っている問題でも大丈夫でしょう。
塾に通うのか、通信教育を行うのかは生活スタイルによっても異なってくるでしょう。子供に負担のかかり過ぎない方法を選ぶようにすると良いです。また、「向き」・「不向き」もあるのでしっかりと見極めるようにしましょう。
算数を得意科目にするには?
算数は闇雲に勉強しても、成績が大幅に向上することはなかなかありません。
そこでタブレット型通信教育などを利用することで効率よく算数の力を鍛えられるでしょう。 子供の実力に合わせて問題が自動で提供される通信教育も存在します。
おすすめの通信教育について詳しい情報はこちらの記事で紹介していますので、ぜひご覧ください。
算数の難問の解き方についてまとめ
算数の難問の解き方についてまとめ
- 難問を経験した場合、他の子供の意見も聞く
- 多くの数の問題を解けば、コツを掴める
- 難問対策には塾や通信講座がおすすめ
算数の難問の解き方について、様々な項目に分けて解説してきました。
難問を必ず解く必要はありませんが、興味を持った場合は挑戦してみても良いです。
小学生の中には、直感的に難問が解ける子供もいます。
しかし、多くの問題に取り組むことで難問が解けることも可能になっています。
中学受験を考えている場合は、積極的に難問に取り組んでみても良いです。
基礎から応用へとしっかりと段取りを取りながら、難問に挑んでいきましょう。







